Предметом рассмотрения дискретной математики являются методы, которые применяются при исследовании, анализе и решении задач управленческого содержания. В таких отраслях экономики, как эконометрика, логистика, математическое моделирование широко используют графы и математическую логику.
Например, в эконометрике булевские переменные применяются в исследовании регрессионных моделей с переменной структурой, а также в построении регрессионных моделей по неоднородным данным. В этом случае рассматривается лишь одно уравнение регрессии, в которое вводятся булевские переменные, характеризующие изучаемый фактор. На наш взгляд, данный метод удобен для выявления зависимости модели от некоторого фактора.
В логистике широко используется теория графов для описания потоков, задания маршрутов. Например, схему дорог удобнее представить в виде ориентированного графа, в котором известными нам методами выбрать кратчайший путь.
Мы полагаем, что в современных условиях, прокладывая маршрут, особое внимание необходимо обратить на пропускную способность магистралей. В данном случае экономически выгодное решение можно получить, интерпретируя маршруты в графы.
Выбор конкурентоспособного товара или услуги можно выбрать с помощью теории нечетных множеств, которая часто применяется в маркетологии при исследовании рынка услуг.
История развития дискретной математики уходит своими корнями в древность, где уже тогда были известны комбинаторно-логические задачи, решение которых происходило путем перебора комбинаций дискретных объектов и логического анализа возникающих вариантов.
Начало развития дискретной математики относят к XVII в. и связывают с появлением работ Л. Эйлера в области комбинаторного анализа и теории графов и Я. Бернулли по комбинаторной теории вероятностей. Огромную роль в развитии идеологии дискретной математики сыграл Г.В. Лейбниц. В XIX веке в области дискретной математики работали такие математики как Ж.Л. Лагранж, А. Кэли, Дж. Буль, К. Жордан и другие.
Примерами дискретных математических объектов могут являться натуральный ряд чисел; конечное множество элементов произвольной природы; слово (последовательность символов) и формальный язык (множество слов) в конечном алфавите; функция (отображение) из конечного множества в конечное множество и другие.
Необходимо отметить, что, с одной стороны, дискретная математика включает в себя такие разделы, как алгебра, теория множеств, теория чисел, математическая логика и другие. С другой стороны, дискретная математика состоит из ряда специальных разделов и сравнительно новых разделов, которые стали активно развиваться с середины XX века. Это связано с изобретением и внедрением во все сферы жизни человека цифровых технологий и ЭВМ.
Дискретная математика послужила основой проектирования цифровых электронных устройств. Первые применения дискретной математики в этой области связаны с именами К.Э. Шеннона, В.А. Котельникова, В.И. Шестакова.
Возникновение математической теории управляющих систем привело к развитию новых разделов дискретной математики, таких как: теория сложности, теория надежности схем, теория автоматов и других. Существенный вклад в дискретную математику на этом этапе был сделан С.В. Яблонским, Дж. фон Нейманом, А.А. Ляпуновым, О.Б. Лупановым.
Начиная с середины XX века, в жизнь современного человека бурно вошли информационные системы. В начале своего развития это были кибернетические системы, затем – системы с интеллектуальными свойствами, определяющими в которых были информационно-логические, дискретные процессы решения различных задач.
На данном этапе развития общество возникло противоречие, которое не позволяло методами классической высшей математики моделировать интеллектуальные и кибернетические системы. В связи с этим, появилась дискретная математика, которая служила для описания главных систем информационного периода.
Роль дискретной математики заключается в определении следующих факторах:
– модели дискретной математики служат хорошим средством построения и анализа моделей в различных науках;
– дискретную математику можно рассматривать как теоретические основы компьютерной математики;
– язык дискретной математики удобен и фактически стал метаязыком современной математики.
В настоящее время знание дискретной математики необходимо специалистам различных сфер деятельности. Интерес к этой дисциплине не случаен. Это обусловлено широким кругом ее применения: электроника, информатика, вопросы оптимизации и принятия решений и т.д.
Например, суждение: «Если цены высокие (А), то и заработная плата должна быть высокой (В). Цены высокие или применяется регулирование цен (С). Если применяется регулирование цен, то нет инфляции (˥D). Инфляция есть. Следовательно, заработная плата должна быть высокой».
Решение. Формулы первых четырех высказываний формируют посылки, а формула пятого высказывания является заключением. Другими словами:
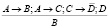 .
.
Посылки и заключения разделены между собой чертой.
|
A |
B |
C |
D |
1→2 |
1∨3 |
4 |
3→7 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
Выделенная строка таблицы показывает, при каких значениях A, B, C и D истинны посылки и заключения.
Анализ таблицы показывает, что заработная плата при высоких ценах и наличии инфляции должна быть высокой и не должно быть регулирование цен.
Приведем еще один пример. Проверить совместность утверждений. Либо свидетель не был запуган, либо, если Герман покончил жизнь самоубийством, записка была найдена. Если свидетель был запуган, то Герман не покончил жизнь самоубийством. Если записка была найдена, то Герман покончил жизнь самоубийством.
Решение. Введем булевы переменные. Пусть x – «свидетель не был запуган», y – «Герман покончил жизнь самоубийством», z – «записка была найдена». Составим конъюнкцию и посмотрим, не является ли она противоречием.
Здесь употреблено выражение «либо…, либо…», поэтому первое составное высказывание следует записать в виде 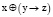 .
.
Это не равно тождественному 0, следовательно, высказывания не являются противоречивыми.
Приведенные выше примеры показывают, что для экономистов большое значение имеет знание классической логики в будущей профессиональной деятельности. На основе знаний законов логики основываются принципы алгоритмизации, лежащие в основе программирования.
Таким образом, дискретная математика играет важную роль в современном мире, так как имеет широкий спектр приложений в различных областях жизнедеятельности человека. Обучение дискретной математике для будущих специалистов экономической деятельности является многофункциональным, многоцелевым, многоуровневым процессом, который состоит во воздействии на элементы системы обучения, а также их связи.
Библиографическая ссылка
Невидомская И.А., Копылова Е.П., Сотникова Ю.Д., Нивинская С.И. ПРИМЕНЕНИЕ ДИСКРЕТНОЙ МАТЕМАТИКИ ПРИ РЕШЕНИИ ЗАДАЧ ЭКОНОМИЧЕСКОГО СОДЕРЖАНИЯ // Современные наукоемкие технологии. 2014. № 5-2. С. 169-171;URL: https://top-technologies.ru/ru/article/view?id=34048 (дата обращения: 05.03.2026).



