Важнейшей ступенью в изучении экономических связей является выяснение их социально- экономической сущности. В практической деятельности не все экономические явления и процессы можно свести к функциональным зависимостям, когда величине факторного показателя соответствует единственная величина результативного показателя.
Стохастические зависимости больше встречаются в экономических исследованиях. Они проявляются только в среднем по значительному количеству объектов или наблюдений и отличаются приблизительностью, неопределенностью. Из этого следует, что каждой величине факторного показателя может относиться несколько значений результативного показателя.
Под корреляционной (стохастической) связью понимается – неполная зависимость между показателями. Она проявляется только в массе наблюдений. Значит, парная корреляция – это связь между двумя показателями, один из которых является результативным, а другой – факторным. Множественная корреляция возникает от взаимодействия с результативным показателем нескольких факторов.
К условия использования корреляционного анализа относятся:
– наблюдений о факторных и результативных показателях, которые исследуются, должно быть в достаточном количестве (по совокупности однородных объектов в динамике или за текущий год);
– анализируемые факторы должны иметь количественное измерение и отражение в электронном или письменном источнике.
Благодаря корреляционному анализу можно решить следующие задачи:
– установить изменение результативного показателя под воздействием лишь только одного или нескольких факторов, то есть узнать, на сколько единиц изменится величина результативного показателя при изменении факторного на единицу;
– найти условную степень зависимости результативного показателя от каждого фактора.
Из этого следует, что идея о взаимосвязи между экономическими переменными, с которой встречается каждый изучающий экономист – первая принципиальная идея.
Рассмотрим ситуации:
Например, спрос на рынке на некоторый продукт понимается как функция его цены; расходы, объединенные с изготовлением какого-либо товара, зависят от объема производства; функцией дохода могут быть потребительские расходы. Это наглядные примеры зависимостей между двумя переменными, одна из которых предполагает потребительские расходы, производственные затраты, спрос на товар и выполняет роль разъясняемой переменной или результирующего значения, а другие трактуются как излагаемые факторы-аргументы. Для достоверности в данное соответствие следует вводить остаточную случайную составляющую, которая отражает влияние на конечный показатель всех непредусмотренных моментов и несколько излагаемых переменных.
В следующей ситуации говориться о том, что даже при одинаковых условиях, увеличение эффективности труда работников способствует различному приросту результатов труда на отдельных предприятиях. Это обусловлено тем, что многие причины – работают в комплексе, взаимосвязано от них зависит производительность труда.
Будет неодинаковая степень воздействия всех факторов на величину результативного показателя, от того насколько приемлемо они сочетаются.
Допустим, что теоретик в области экономической науки определил следующие утверждения:
– функция потребления всегда растёт быстрее по сравнению с получаемыми доходами;
– при увеличении объёма инвестиций, функция национального дохода возрастает, а функция, характеризующая государственное регулирование убывает;
– сумма государственных и инвестиционных услуг и товаров, а также потребительских закупок – есть величина национального дохода.
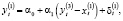
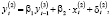
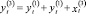
Выразить эти положения математическим языком составляет главную задачу. И сейчас же мы встречаемся с множеством всевозможных способов удовлетворения открывающихся перед нами, сформулированных требованиями теоретика-экономиста. Какому соответствию переменных отдать предпочтение – нелинейным или линейным? Если выбрать нелинейные, то следует, они должны быть – полиномиальными логарифмическими, либо ещё какими-нибудь. Проблема выбора остаётся нерешённой для разнородных уравнений запаздываний по времени, даже установив форму определённого соответствия. Остаётся открытым вопрос, например, скажется ли на долгосрочные вложения капитала динамика предшествующих периодов, или же они будут реагировать исключительно на национальный доход, который был произведён в конечном периоде. Простой выход из этих затруднений заключается в выборе при исходном анализе самой простой из допустимых форм этих соотношений. Тогда основе установленных положений возникает вероятность записать аддитивную относительно случайных образующих модель и линейную относительно исследуемых переменных: где априорные границы выражены неравенствами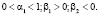 
Эти три соответствия вместе с ограничениями образуют модель. Так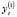 
определяет потребление, 
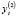– инвестиции, 
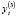– национальный доход, 
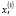– налог на доходы физических лиц, 
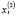– ставка процента, выступающий инструментом государственного регулирования, 
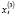– государственные закупки продукции и услуг, фиксированные в момент времени. Наличие в данных уравнениях случайных (остаточных) элементов 
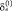и 
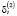определено потребностью принять к сведению влияние в применении на и ряда непредусмотренных факторов. В самом деле, не всегда ожидаемо, количество потребления будет прямо устанавливаться уровнями национального дохода (
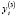) и налогом на доходы физических лиц (
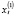); подобно величина инвестиций 
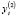обусловлена, несомненно, не только достигнутым в предшествующий год уровнем национального дохода 
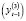и величиной ставки процента 
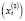, но и от ряда не принятых во внимание в уравнении факторов. Данная модель включает два уравнения и одно тождество, раскрывает поведение инвесторов и потребителей. Модель выражена для дискретных промежутков времени и имеет отставание или лаг в один момент для отражения влияния национального дохода на инвестиции. Этот пример освещает совокупные свойства одного из значительных этапов эконометрического моделирования, в ходе которого исследователь математически анализирует некоторые концепции экономической теории и интегрирует их в систему.
Статистическое исследование зависимостей включает следующие методы:
– анализ параметров системы малодоступных для непосредственного измерения и наблюдения;
– анализ эффективности или качества работы рассматриваемой системы;
– нормирование;
– регулирование, наиболее соответствующее определённым условиям и задачам, величин функционирования анализируемой системы, ситуационный анализ;
– планирование, прогноз, диагностика.
Прогнозирование социально-экономических систем в большей части случаев разрабатывается посредством стохастического аппарата, поэтому данный прогноз имеет стохастическое направление. Это и диктует определение промежутка времени, в котором с объективной возможностью будет находиться анализируемая величина. Предположим, эта величина в последующем используется как входная переменная, то принято, что она может быть в центре доверительного интервала.
Действующие в данное время способы проверки качества прогноза довольно формальны и могут использоваться лишь только, когда ныне анализируемый период оказывается отчётным. Поэтому целесообразно применять методы, определяющие качество прогноза в нынешних условиях или, по крайней мере, сравнивают качество некоторых прогнозов.
В заключение можно сказать, что изучение корреляционных соотношений имеет огромное значение в анализе хозяйственной деятельности и в экономических процессах. Это выражается в том, что в большей степени расширяется факторный анализ, формируется роль и место всех факторов в установлении уровня анализируемых показателей, растут знания об изучаемых явлениях, вырабатывается правильность их развития и как итог – точнее составляются управленческие решения и планы, более справедливо оцениваются результаты деятельности предприятий, а также устанавливаются внутрихозяйственные запасы.
Библиографическая ссылка
Найденова Ю.А., Долгополова А.Ф. ОСОБЕННОСТИ СТОХАСТИЧЕСКИХ ЗАВИСИМОСТЕЙ В ЭКОНОМИКЕ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 168-169;URL: https://top-technologies.ru/ru/article/view?id=34047 (дата обращения: 19.04.2024).