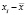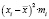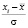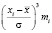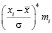В любой науке основной задачей является выявление и исследование закономерностей, которым подчиняются процессы, происходящие в реальном мире. Эти процессы имеют не только теоретическую направленность, они широко применяются на практике, в частности, в планировании, управлении и прогнозировании.
При исследовании многих явлений, в том числе экономических, необходимо учитывать не только основные факторы, но и множество второстепенных, приводящих к случайным событиям. Наука, направленная на изучение случайных, не подлежащих строгому математическому описанию событий и явлений, их свойств, закономерностей и взаимосвязей, называют теорией вероятностей.
Теория вероятностей изучает объективные закономерности массовых случайных событий. Она является теоретической базой для математической статистики, занимающейся разработкой методов сбора, описания и обработки результатов наблюдений.
Например, на финансовом рынке непрерывно заключается большое количество сделок и торговых операций. Некоторые из них в дальнейшем приведут к убытком, а другие могут принести прибыль. Точно сказать последствия совершаемых операций невозможно. Их результат зависит от множества непредсказуемых факторов.
Статистические исследования 60 различных финансовых сделок определили распределение прибыли в млн.руб. Данные сведены в таблицу. Необходимо определить моду, медиану, среднее квадратическое отклонение, дисперсию, коэффициент вариации.
Таблица 1
Дано распределение 60 финансовых сделок по получаемой прибыли, млн. руб.
|
Номер интервала |
Границы интервала |
Частота, mi |
Накопленная частота, miнак |
Частость, wi |
Накопленная частота, wiнак |
|
1 |
0,2;0,8 |
1 |
1 |
1/60 |
1/60 |
|
2 |
0,8;1,5 |
1 |
2 |
1/60 |
2/60 |
|
3 |
1,5;2,2 |
7 |
9 |
7/60 |
9/60 |
|
4 |
2,2;2,8 |
16 |
25 |
16/60 |
25/60 |
|
5 |
2,8;3,5 |
18 |
43 |
18/60 |
43/60 |
|
6 |
3,5;4,2 |
11 |
54 |
11/60 |
54/60 |
|
7 |
4,2;4,9 |
4 |
58 |
4/60 |
58/60 |
|
8 |
4,9;5,5 |
2 |
60 |
2/60 |
1 |
Максимальное значение частоты mmax = 18, соответствует интервалу [2,8; 3,5).
Тогда значение моды определим по формуле
.
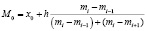Таким образом,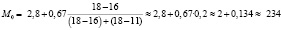 
Так как объем выборки n=60, то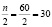 
, значит находим интервал, соответствующий частоте большей 30. Это miнак = 43.
Следовательно медиана расположена в интервале [2,8; 3,5). Тогда x0=2,8, mi-1нак =25, mi-1=16.
Медиана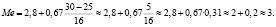 
Выборочная средняя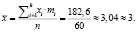 
Выборочная дисперсия
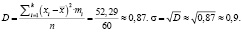
Тогда V – коэффициент вариации равен: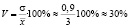 
.
Для нахождения других характеристик составим вспомогательную таблицу
|
Границы интервала |
Среднее значение интервала xi |
Частота, mi |
xi· mi |
|
|
|
|
|
|
0,2;0,8 |
0,5 |
1 |
0,5 |
-2,5 |
6,25 |
-2,8 |
-21,952 |
61,46 |
|
0,8;1,5 |
1 |
1 |
1 |
-2 |
4 |
-2,2 |
-10,648 |
23,42 |
|
1,5;2,2 |
1,8 |
7 |
12,6 |
-1,2 |
10,08 |
-1,3 |
-15,379 |
19,99 |
|
2,2;2,8 |
2,5 |
16 |
40 |
-0,5 |
4 |
-0,6 |
-3,456 |
2,07 |
|
2,8;3,5 |
3,2 |
18 |
57,6 |
0,2 |
0,72 |
0,2 |
0,144 |
0,03 |
|
3,5;4,2 |
3,8 |
11 |
42,3 |
0,85 |
7,95 |
0,9 |
8,019 |
7,22 |
|
4,2;4,9 |
4,5 |
4 |
18,2 |
1,55 |
9,61 |
1,7 |
19,652 |
33,41 |
|
4,9;5,5 |
5,2 |
2 |
10,4 |
2,2 |
9,68 |
2,7 |
27,648 |
66,36 |
|
Итого |
- |
60 |
182,6 |
-1,4 |
52,29 |
- |
4,028 |
213,96 |
Таким образом, среднее значение полученной прибыли от реализованной продукции составляет 3 млн.рублей. Плотность результатов в среднем колебалась в промежутке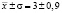 
, то есть от 2,1 до 3,9. Данный интервал, а также коэффициент вариации показывает, что имеются большие различия в полученной прибыли.
Библиографическая ссылка
Манастырная Е.С., Невидомская И.А. ТЕОРИЯ ВЕРОЯТНОСТЕЙ КАК ТЕОРЕТИЧЕСКАЯ ОСНОВА МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 165-166;URL: https://top-technologies.ru/ru/article/view?id=34045 (дата обращения: 22.11.2024).