В моделировании экономических процессов роль интеграла рассматривается не так часто, но, не смотря на это интегральное исчисление, для моделирования и исследования процессов, происходящих в экономике дает богатый математический аппарат. Вычисление площадей различных фигур, нахождение объемов геометрических тел и некоторые приложения в физике и технике иллюстрируются приложением интеграла.
Остановимся на некоторых примерах использования интегрального исчисления в экономике. Для начала рассмотрим понятие потребительского излишка в рыночной экономике. И поэтому рассмотрим некоторые экономические понятия и обозначения.
Спрос на данный товар – это сложившаяся зависимость между объемом покупки и ценой товара на определенный момент времени. Графически спрос на отдельный товар изображается в виде кривой с отрицательным наклоном, которая отражает взаимосвязь между количеством товара Q и ценой P единицы этого товара и, которое потребители готовы купить при каждой заданной цене. Отрицательный наклон кривой спроса имеет следующее объяснение: чем дороже товар, тем меньше количество товара, которое покупатели готовы купить, и наоборот.
Рассмотрим понятие, которое играет в моделировании экономических процессов большую роль – рыночное равновесие. Состояние равновесия характеризуют: количество и цена, при которых объем спроса совпадает с величиной предложения, а графически это изображается точкой пересечения кривых спроса и предложения (рис. 1).
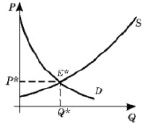
Рис. 1
Далее для удобства разбора мы начнем рассматривать обратные функции спроса и предложения, которые характеризуют зависимость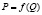 
, а не зависимость 
.
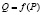Теперь для определения потребительского излишка рассмотрим приложения интегрального анализа. Для этого на графике изобразим обратную функцию спроса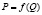 
. Предположим, в точке 
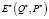установилось рыночное равновесие (на графике отсутствует кривая предложения для удобства дальнейшего анализа) (рис. 2).
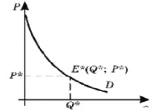
Рис. 2
Если покупатель по равновесной цене P*, приобретает товар в количестве Q*, то, следовательно, что расходы общие на покупку такого товара составят P*Q*, и это на графике соответствует площади заштрихованной фигуры A (рис. 3).
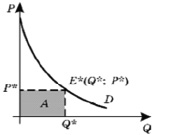
Рис. 3
Но представим, что товар в количестве Q* продавцами продается не сразу, а небольшими партиями Q поступает на рынок. То есть такое допущение совместно с непрерывностью функции спроса и предложения при выводе формулы является для расчета потребительского излишка основным.
Расчет потребительского излишка – это разность между максимальной суммой денег, которую потребитель готов и согласен за купленное количество благ заплатить, и суммой денег, которую фактически он заплатил за товар.
Таким образом, посчитать потребительский излишек можно по следующей формуле:
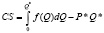(1)
Рассмотрим задачу на определение излишка потребителя.
Пусть известно, что на некоторый товар спрос задается функцией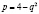 
, где q – количество товара (в шт.), p – цена единицы товара (в руб.), а при 
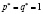достигается равновесие на рынке данного товара. Необходимо определить величину потребительского излишка.
Решение.
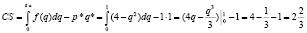(руб.).
Рассмотрим оценку последствий введения потоварного налога.
В предложении, где существует единственная возможность производства продукта, введение потоварного налога приводит к нужному результату, и при этом объем выпуска и размер внешнего эффекта, несомненно, связаны друг с другом.
После введения потоварного налога уменьшается объем как потребления, так и производства. Помимо этого, более высокую цену платят покупатели, а более низкую получают относительно первоначальной равновесной цене. Поэтому, налог ухудшает экономическое положение и продавцов, и покупателей.
Дана кривая спроса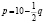 
. Каковы денежные затраты потребителя при введении налога на данный товар с единицы продаж в размере 1 руб., когда известно, что при цене 
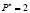руб. наблюдалось первоначальное рыночное равновесие на этом рынке.
Эту задачу можно решать и другими способами. Проиллюстрируем два основных способа решения данной задачи.
Первый способ. Чтобы определить потребительские потери при увеличении 2 руб. до 3 руб. равновесной цены товара, посмотрим, как меняется при этом объем продаж. Если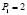 
, то 
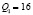, при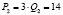 
. Следовательно,
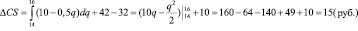
Второй способ. Поскольку функция спроса в данном случае линейна, то ситуацию, которую мы рассматриваем легко представить графически (рис. 4).
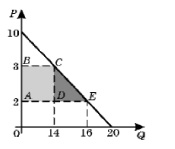
Рис. 4
Получим, что
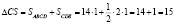(руб.).
Второй способ решения легче первого и знаний математического анализа, особых не требуется. Общий метод нахождения, при помощи определенного интеграла, изменения потребительского излишка, поясняет сущность функции спроса и предложения.
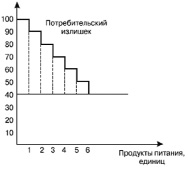
Рис. 5
Допустим, что цена продуктов 30 р. за кг. Цена первого кг равна 30 р., но его «ценность» для потребителя – 90 р. Чтобы определить «ценность» необходимо использовать кривую спроса, позволяющую поставить максимальную цену, которую с целью приобретения дополнительной единицы продуктов питания потребителю необходимо уплатит. Продукты можно приобрести, так как его цена меньше максимальной цены на 60 р., и дает оно избыточную стоимость. Второй кг продовольствия также стоит покупать, так как это дает избыточную стоимость в 50 р. (80 р. – 30 р.). Третий кг дает излишек в 40 р. (70 р. – 30 р.). Четвертый кг дает излишек в 30 р., пятый – в 20 р., шестой – в 10 р. Седьмой кг продовольствия питания дает нулевой излишек. Каждый следующий кг имеет ценность, которая меньше его цены, поэтому потребитель не предпочитает приобретать больше продуктов питания. Сложением избыточной стоимости по всем приобретаемым единицам получается излишек потребителя. Исходя из этого, совокупный излишек потребителя составляет: <<prilmat429.wmf>>.
Таким образом, рассмотренные нами основные способы решения широко применяются на практике. Экономисты вычисляют в зависимости от различных вариантов налогообложения изменения потребительских излишков, и с учетом необходимого размера налоговых поступлений анализируют полученные результаты, останавливаются на тех вариантах, которые вызывают наименьшее сокращение потребительских выгод.
А при складывании многих отдельных излишков совокупную выгоду измеряет совокупный излишек потребителя, которую приобретают потребители, при покупке товары на рынке. Определить прибыль альтернативных рыночных структур и издержки позволяют, соединение прибыли и излишка потребителя, определяющих поведение, как потребителей, так и производителей на рынке. Следовательно, в экономике концепция излишка потребителя имеет огромное значение.
Таким образом, определенный интеграл определяет практическую роль при решении экономических задач, так как позволяет найти правильное решение при минимальных затратах времени и сил.
Библиографическая ссылка
Зарвирова М.С., Хаджиназарова А.С., Родина Е.В. РОЛЬ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА В ЭКОНОМИКЕ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 156-158;URL: https://top-technologies.ru/ru/article/view?id=34038 (дата обращения: 23.11.2024).