Структурная форма модели (системы одновременных уравнений) – это система уравнений, в каждом из которых помимо объясняющих (независимых) переменных могут содержаться объясняемые (зависимые) переменные из других уравнений. Уравнения, составляющие исходную модель, называются структурными уравнениями модели.
Простейшая структурная форма модели имеет вид:
,
,
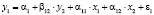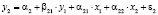где y1, y2 и x1, x2 – зависимые и независимые переменные; ε1 и ε1 – случайные слагаемые;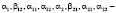 
параметры модели.
Параметры структурной формы модели называются структурными коэффициентами.
Структурная форма модели включает в систему не только уравнение, отражающее взаимосвязи между отдельными переменными, но и уравнения, отражающие тенденцию развития явления – функции времени, а также разного рода уравнения-тождества. Тождества не содержат каких-либо подлежащих оценке параметров, а также не включают случайных слагаемых.
Структурные коэффициенты можно однозначно выражать через приведенные коэффициенты, или они могут иметь несколько разных оценок, но совсем не выражаться через них.
В процессе оценивания параметров одновременных уравнений следует различать эндогенные (внутренние, зависимые) и экзогенные переменные. Эндогенными считаются переменные, значения которых определяются внутри модели. Это зависимые переменные, число которых равно числу уравнений системы. Экзогенными (внешними, независимыми) считаются переменные, значения которых определяются вне модели. Это заданные переменные, влияющие на эндогенные переменные, но не зависящие от них.
Структурный коэффициент называется идентифицируемым, если его можно точно вычислить на основе приведенных коэффициентов, точно идентифицируемым, если он имеет единственную оценку, и сверхидентифицируемым, если он имеет несколько разных оценок. В противном случае он называется неидентифицируемым.
Структурное уравнение является идентифицируемым, если идентифицируемы все его коэффициенты. Если хотя бы один структурный коэффициент неидентифицируем, то и все уравнение является неидентифицируемым.
Модель считается идентифицируемой, если каждое ее уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель является неидентифицируемой.
В случае неидентифицируемости структурной модели в нее необходимо ввести новые переменные, с помощью которых можно было бы добиться идентифицируемости модели. Рассмотрим модель спроса и предложения:
уравнение спроса: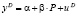 
,
уравнение предложения: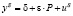 
,
тождество равновесия: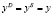 
,
где P – цена товара; a, b, g и e – параметры; uD и us – случайные слагаемые.
Переменные y, P являются эндогенными, их значения определяются в процессе установления рыночного равновесия.
В рассматриваемой модели нет экзогенных переменных, поэтому ни одно из этих уравнений не является идентифицируемым. Чтобы модель имела статистическое решение, в нее необходимо ввести экзогенные переменные.
Если все продавцы товара облагаются специальным налогом T, который они должны платить с выручки, то данные об этом налоге могут быть включены в состав данных, используемых для анализа. При этом уравнения спроса останется неизменным, если переменная P означает рыночную цену, а уравнение предложения изменится. Система примет вид:
уравнение спроса: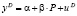 
,
уравнение предложения: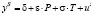 
,
тождество равновесия: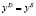 
,
где T – экзогенная переменная; s –дополнительный параметр.
Уравнение спроса будет идентифицируемым, поскольку переменная T не включена в него и может выступать в качестве инструментальной для переменной P, а уравнение предложения – неидентифицируемым.
В уравнение спроса можно включить переменную x – доход на душу населения, при этом система примет вид:
уравнение спроса: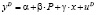 
,
уравнение предложения: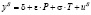 
,
тождество равновесия: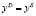 
,
где x – экзогенная переменная – доход на душу населения; g –дополнительный параметр.
Экзогенную переменную x можно использовать в качестве инструментальной переменной для уравнения спроса. В итоге полученная модель представляет собой точно идентифицируемую модель спроса и предложения.
В некоторых случаях неидентифицируемая модель может быть превращена в идентифицируемую путем задания соотношения между структурными коэффициентами. Такой метод носит название метода ненулевого ограничения. Рассмотрим этот метод на примере неидентифицируемой модели спроса и предложения:
уравнение спроса: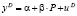 
,
уравнение предложения: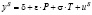 
,
тождество равновесия: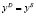 
,
где P – цена товара; T – экзогенная переменная – налог с продаж; a, b, d, e и s –параметры; uD и us – случайные слагаемые.
Улучшить спецификацию модели можно, введя ограничение на коэффициенты s=–e. Тогда система исходных данных – структурных уравнений преобразуется к виду:
уравнение спроса: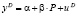 
,
уравнение предложения: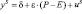 
,
тождество равновесия: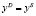 
.
Благодаря введению ограничения на коэффициенты уравнение предложения стало идентифицируемым. Действительно, преобразованную систему можно рассмотреть как новую версию модели – систему из 4 уравнений:
уравнение спроса: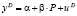 
,
уравнение предложения: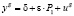 
,
тождество цены товара для продавца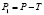 
,
тождество равновесия: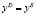 
,
где P1 – цены товара для продавца (сумма, остающаяся у продавца после уплаты налога).
Последние два уравнения системы являются уравнениями-тождествами и не требуют проверки на идентификацию. Переменная T не включена в уравнение спроса, поэтому она может быть использована в качестве инструментальной для переменной P. В результате с помощью метода наименьших квадратов можно получить уравнение регрессии вида:
,
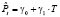где γ0 и γ1 – коэффициенты, подлежащие оценке.
Так как переменная T не включена в уравнение предложения, то она также может использоваться в качестве инструментальной для переменной P1. Полученная модель в целом является точно определенной (точно идентифицируемой).
Таким образом, наличие ограничения на коэффициенты системы уравнений (называемого ненулевым ограничением) позволяет исключить одну объясняющую переменную из уравнения. Если эта переменная эндогенная, для нее не нужно искать инструментальную переменную; если экзогенная, то она может использоваться в качестве инструментальной для одной из эндогенных переменных, оставшихся в уравнении.
Модель спроса и предложения также можно использовать:
– когда необходимо установить характер изменения издержек производства, если известен вид функции затрат;
– когда надо найти предельные издержки производства при данном объеме выпуска, если известна функция затрат;
– когда необходимо установить зависимость спроса от цены на него;
– при нахождении предельного спроса на товар при данной цене, если известна зависимость спроса на товар от цены на него.
Библиографическая ссылка
Донец З.Г., Боташева Л.Р., Гочияева А.К. ПРИМЕНЕНИЕ МОДЕЛИ СПРОСА И ПРЕДЛОЖЕНИЯ В СТРУКТУРНОЙ ФОРМЕ МОДЕЛИ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 153-155;URL: https://top-technologies.ru/ru/article/view?id=34036 (дата обращения: 22.11.2024).