Матрицей размера m×n называется прямоугольная таблица из чисел, содержащая m строк и n столбцов и имеющая вид:
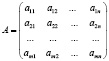
Нам известны основные операции над матрицами: равенство матриц; транспонирование; сложение; умножение матрицы на число; умножение матрицы на матрицу.
Вообще, можно сказать, что матрица – это математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля.
Матрицы впервые появились в середине ХVIII столетия в работах английских математиков А. Кэли и У.Р. Гамильтона. А уже общественный вклад в разработку общей теории матриц внесли русские математики А.Н. Крылов, Лапло-Данилевский.
Как показывает практика, современному экономисту необходима основательная математическая подготовка. В число наиболее важных математических дисциплин для экономиста входит линейная алгебра, а именно матричная алгебра. Это обусловлено тем, что экономико-математические модели, которые широко применяются сейчас в исследовательской и плановой работе, часто предназначены для описания взаимосвязи экономических структур, их динамики во времени, зависимости от ряда факторов. Одним из наиболее компактных, удобных в применении способов является матричное отображение, что позволяет формализовать поставленную проблему.
Благодаря простоте формы и богатому экономическому содержанию матричные методы находят широкое применение в экономической практике: статистические расчёты, организация нормативного хозяйства, сокращение документооборота, организация внутрипроизводственного хозрасчёта и для экономического анализа.
Матричные методы можно также использовать для моделирования экономики отраслей народного хозяйства, экономики республик, народного хозяйства страны. Матрицы данного типа носят название межотраслевого баланса и находят широкое применение в планировании и статистике.
Исходя из этого, можно сделать вывод, что в экономической деятельности, в большей степени, используется метод анализа. Такой метод применяется для целей анализа сложных и многомерных экономических явлений. Чаще всего эти методы используются при необходимости сравнительной оценки функционирования организаций и их структурных подразделений. Следовательно, матричный метод в экономике – это метод научного исследования свойств объектов на основе использования правил теории матриц, по которым определяется значение элементов модели, отражающих взаимосвязи экономических объектов. Используется в тех случаях, когда главным объектом исследования являются балансовые соотношения затрат и результатов производственно – хозяйственной деятельности и нормативы затрат и выпусков. Рассмотрим на примере самое простое применение матрицы в отраслях экономики.
|
Ресурсы |
Угольная промышленность |
Здравоохранение |
|
Электроэнергия |
10,2 |
6,1 |
|
Трудовые ресурсы |
7,8 |
3,5 |
|
Водные ресурсы |
4 |
1,2 |
Упрощённая запись предложенных аналитических данных выглядит следующим образом:
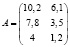
Решение экономических задач, осуществляемое матричным методом позволило решать основные задачи экономического профиля на любом из предприятий.
Пусть предприятие выпускает продукцию трёх видов (P1, P2, P3), использует сырьё двух типов (S1, S2), а нормы расхода:
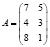, C=(50 60 150).
Стоимость единицы каждого типа сырья (ден.ед) представлена матрицей-столбцом: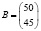 
.
Решая данную задачу аналитически, получаем: – затраты 1-го сырья составляют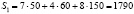 
(ед.);
– затраты 2-го сырья составляют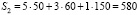 
(ед.);
поэтому матрица-строка затрат сырья S может быть записана как произведение:
S=CA,
где S – затраты сырья; С – заказ; A – матрица производства.
.
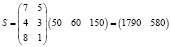Общая стоимость сырья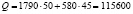 
(ден.ед.) может быть записана в матричном виде:
,
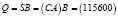где Q – общая стоимость; B – стоимость единицы сырья; S – затраты сырья.
Применение матриц в экономике не может обойтись и без матрицы Абеля, т.к. она позволяет рассматриваемую отрасль какой-либо деятельности компании, привести к критериям выбора конкурентоспособности в технологиях синергетического эффекта и маркетинга.
Например, поступление товаров на первый склад описывается матрицей
,
а поступление товаров на второй склад описывается матрицей
.
Найдите суммарный завоз товаров на склады; годовой завоз на склады, если по договору, производится ежемесячный завоз одинаковых партий товаров.
Решение:
Найдём суммарный завоз
.
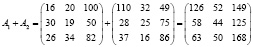Найдём годовой завоз
.
Ответ: 
Простота использования матриц, как в науке, так и на практике играет важную роль в решении экономических задач. Матричный метод сокращает работу человека по заполнению матриц парных сравнений, и это очень важно для решения задач с большим количеством критериев и альтернатив. Также с помощью матричного метода человек получает готовый и обоснованный ответ в виде рейтинга альтернатив по всем критериям, а также ему предлагается самому оценить альтернативы и проверить соответствующие готовые решения исходя из самостоятельного анализа глобальной матрицы альтернатив по всем критериям.
Библиографическая ссылка
Блинова Ю.Ю., Родина Е.В. РЕШЕНИЕ ЭКОНОМИЧЕСКИХ ЗАДАЧ МАТРИЧНЫМ МЕТОДОМ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 140-142;URL: https://top-technologies.ru/ru/article/view?id=34028 (дата обращения: 22.11.2024).