Взаимосвязь между музыкой и математикой вызывала интерес с древних времен. Это и неудивительно, так как в музыке математический компонент проявляется явно.
Математическая наука и музыка имеют много общего. Древнегреческий философ Пифагор первым обнаружил эту замечательную связь. Он создал учение о звуке, рассмотрел звук в философско-математическом аспекте, и даже пытался связать его с астрономией. Последователи Пифагора сделали предположение о том, что в основе мира лежит определенная абстракция – число. Используя специальный инструмент – монохорд, Пифагор определил интервалы звука и открыл математические связи между отдельными звуками. Пифагором было развито учение о лечении заболеваний музыкой. По его мнению, определенные отчетливые мелодии могут избавить людей от ревности, зависти, гордыни и других недостатков. Искусство всего мира многим обязано математике. Тому примеры – разные произведения архитектуры, тренировка животных в цирке с помощью звуков, ультразвуковое исследование в медицине и т.д.
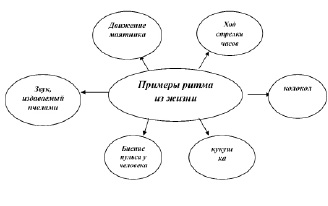
Окружающая нас среда полна ритма. Понятие «Ритм» означало у древних греков чередование равномерных звуков, исполняемых в определенной последовательности. Поэтому он проявляется в любой сфере нашей повседневной жизни. Например, день сменяется ночью, зима – весной, а также ходьба, дыхание человека, стук колес поезда и т.д. звучат ритмично.
При упоминании слова «Ритм», на ум приходит слово «Музыка», так как ритм является наиважнейшим элементом музыки. Ритм – основа всего музыкального движения, гармоничная последовательность по времени всех элементов языка музыки: мелодии, гармонии и т.д.
Поэтесса-лирик, заслуженный деятель в области культурно-просветительской работы, народная писательница Фариза Онгарсынова удачно воспела значение ритма в одном из своих стихотворений.
...Өмір – ырғақ, нәзік әуен, асқақ үн,
айдын, дала, аспан – үн!
Ғұмыры жоқ ырғақтардан басқаның!
Ей, адамзат, бас әуенге, қос әнге,
шырқат биік тіршіліктің дастанын!
Өмір – ырғақ, әуеніне ермесең,
тірлігің – тұл, тас – жаның!
Ғұмыры жоқ ырғақтардан басқаның! [2]
И математика полна ритма. Возьмем ряд натуральных чисел: 1,2,3,4,5.… Чувствуется ритм. Его основа – каждое следующее число, которое получается путем прибавления единицы к предыдущему числу. Также к ритму относится маршировка военнослужащих, при подаче команды движении со счетом вслух – раз, два, три.
В музыке существуют акценты, основанные на чередовании сильных и слабых долей. Ударный слог называется сильной долей, безударный слог – слабой долей. Промежуток между двумя сильными долями называется тактом и отделяется двумя вертикальными линиями. Первая доля всегда бывает сильной. В каждом такте бывают одна сильная и три слабые доли. В зависимости от количества долей в такте размеры делятся на простые (двух- или трехдольные), сложные (четырех-, шести-, девяти-, двенадцати дольные) и смешанные (пятидольные). Размер такта обозначается дробью, в которой числитель обозначает количество долей, а знаменатель – вид доли (в зависимости от продолжительности). Простые размеры обозначаются дробью в виде 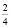 ,
, 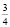 . Размеры, образующиеся в результате сложения двух- или трехдольных простых размеров, называются сложными размерами. Они обозначаются в виде
. Размеры, образующиеся в результате сложения двух- или трехдольных простых размеров, называются сложными размерами. Они обозначаются в виде 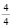 ,
, 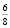 . Если в математике дроби
. Если в математике дроби 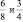 равны, то в музыке они не равны. [1]
равны, то в музыке они не равны. [1]
В качестве основы размера 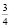 берется продолжительность
берется продолжительность 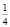 , а основы размера – продолжительность
, а основы размера – продолжительность 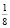 . К сложным размерам относятся четырех-, шести-, девяти-, двенадцатидольные размеры. Помимо простых и сложных размеров, существуют смешанные размеры. Сочетание двухдольного и трехдольного простого размера называется смешанным размером.
. К сложным размерам относятся четырех-, шести-, девяти-, двенадцатидольные размеры. Помимо простых и сложных размеров, существуют смешанные размеры. Сочетание двухдольного и трехдольного простого размера называется смешанным размером.
Например: 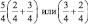
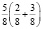 или
или 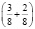
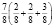 или
или 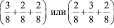
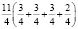 или
или 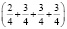
В музыке число 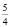 в записи
в записи 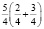 обозначает результат сложения двух дробей в скобках, а в математике такая запись обозначает результат произведения двух дробей.
обозначает результат сложения двух дробей в скобках, а в математике такая запись обозначает результат произведения двух дробей.
В математике ритм используется в качестве синонима к слову «закономерность».
Если превратить число в десятичную дробь, то получим – 0,166666666...
В данном случае закономерность проявляется в периодическом повторении числа 6. Из курса математики мы знаем, что написание периодической дроби 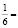 0,1(6). Таким же образом:
0,1(6). Таким же образом:
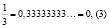
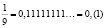
И наоборот, знаем правила перевода периодических дробей в обыкновенную.
0,27272727...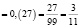
Среди чисел можно также наблюдать ритм. Кратные числа в математике могут быть примерами ритма. Если указать первые 100 натуральных чисел в виде таблицы Пифагора, состоящей из 10 строк и 10 столбцов, то увидим, что первые цифры чисел, стоящих в одной строке, совпадают со вторыми цифрами чисел этой строки. Таким же образом можно сравнить графики функции с музыкальным ритмом и выявить их связь. Особенно можно отметить графики тригонометрических функций – синусоида, косинусоида.
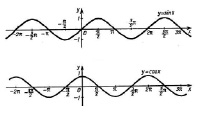
Известно, что контрарные пары встречаются и в математике, и в музыке.
В качестве еще одного примера, показывающего связь музыки с математикой является закон Золотого сечения. Первоначальные понятия о «Золотом сечении» среди математиков рассматривались в «Началах» Евклида. Закон Золотого сечения, получивший распространение в связи с решением геометрической задачи «Деление отрезка в среднем и крайнем отношении», встречается также в музыке. На практике было установлено, что при длине струны равной 0,6, получаются приятные, мелодичные звуки, говоря языком музыкантов, гармонический аккорд. Аккорд (итал. «согласование, гармония») – это созвучие трех и более звуков, слышимых одновременно, расположенных в определенном порядке.
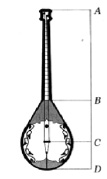
Если обратить внимание на казахский национальный инструмент – домбру, можно заметить наличие всех частей, сохраняющих закон Золотого сечения. Об этом можно найти в трудах К.Н. Нурсултанова [3].
Математика является наукой, развивающей и совершенствующей мышление, основным ключом к мировоззрению. Значение математики в любой сфере науки огромно. Это и проявляется из связи между музыкой и математикой. Применение математической теории в музыке позволяло Пифагору создавать особые музыкальные мелодии, являвшиеся наслаждением для души. В школе можно проводить внеклассные работы на данную тему. Такие внеклассные работы реализуют межпредметные связи, воспитывают в учениках такие качества, как трудолюбие, сплоченность, нравственность. Определение общих закономерностей в математике и музыке развивает логическое и абстрактное мышление учеников, формирует эстетическое мировоззрение. Это обусловливает то, что математика занимает особое место в искусстве.
Библиографическая ссылка
Берикханова Г.Е., Баймурзаева А.Б. МАТЕМАТИЧЕСКОЕ ОБОСНОВАНИЕ МУЗЫКАЛЬНОГО РИТМА // Современные наукоемкие технологии. 2014. № 5-2. С. 138-140;URL: https://top-technologies.ru/ru/article/view?id=34027 (дата обращения: 05.03.2026).



