Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы
• Литература

Агафонова Н.П. 1 Орехова Н.В. 1 Мелешко С.В. 1

---

1 Ставропольский государственный аграрный университет

Статья в формате PDF

1157 KB

1. Замков О.О., Толстопятенко А.В., Черемных Р.Н. Взвешенный метод наименьших квадратов.– Математические методы в экономике. – М.: Дис, 1997.

2. Мамаев И.И., Бондаренко В.А. Функции нескольких переменных в моделировании экономических процессов // Аграрная наука, творчество, рост. – Ставрополь, из-во «АГРУС», 2013. – Т.1,Ч.1. – С. 286.

3. Родина Е.В., Саакян Л.Г., Федорец Н.П. Экономический смысл производной //Современные наукоемкие технологии. – 2013. № 6. С. 83-84.

4. Экономическая теория: учебник под редакцией Е.Н. Лобачевской – 2-е изд., Москва. Высшее образование, 2008.

3. Донец З. Г.,Мамаев И. И., Шибаев В. П.Учебная организация как целостная модель организации обучения студентов на интегративной основе//Теоретические и прикладные проблемы современной педагогики : сборник научных статей по материалам научно-практической конференции. – Ставрополь: изд-во «АГРУС», 2012. – С. 40-48.

Математика – царица наук. Это выражение вовсе не случайно, ведь математика играет огромную роль в развитии всех остальных наук. Но наибольшее влияние она оказывает на смежные науки, такие как: экономическая теория, политэкономия, макроэкономика, микроэкономика.

В нашей статье мы хотим раскрыть взаимосвязь микроэкономики и математики.

Рынок, с точки зрения купли продажи, – это сфера взаимодействия спроса и предложения. Из этого следует вывод, что спрос и предложение являются основными составляющими рынка. В их взаимодействии формируются цены на различные товары и услуги. Экономическая наука занимается изучением механизма их взаимодействия. Для этого спрос и предложение отображаются графически, т.е. на основании полученных данных на координатной плоскости откладываются точки, где у – значение цены, а х – объем спроса или предложения. Но математика позволяет на основании этих данных составить уравнение функции, для этого используется метод наименьших квадратов.

До начала XIX в. учёные не имели определённых правил для решения системы уравнений, в которой число неизвестных меньше, чем число уравнений. До этого времени применялись частные приёмы, зависевшие от вида уравнений и от логики вычислителей, и потому разные математики, приходили к различным выводам. Гауссу, в 1795 году, принадлежит первое применение метода, а Лежандр, в 1805 году, независимо от Гаусса открыл и опубликовал этот же метод. Лаплас связал метод с теорией вероятностей, а американский математик Эдрейн рассмотрел его теоретико-вероятностные приложения. Метод распространён и усовершенствован дальнейшими изысканиями Энке, Бесселя, Ганзена и других.

Сущность этого метода заключается в следующем: из множества формул вида y=f(x) наилучшим образом изображающей взятые значения лучшей считается та, для которой сумма квадратов отклонений, наблюдаемых значений от вычислений, является наименьшей.

Применение метода заключается в следующем:

– согласно данным эксперимента откладываем на координатной плоскости точки;

– определяем с графиком, какой функции схож получившийся график (линейная, квадратичная, гиперболическая, показательная и т.д.);

– предположим, что функция имеет вид 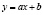, нам необходимо найти значения a и b;

– параметры будем определять таким образом, чтобы сумма квадратов отклонений вычисленных значений от наблюдений принимала наименьшее значение:

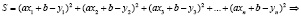
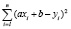– наименьшие значения.

На основании предыдущей формулы можно сделать вывод, что 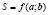является функцией двух переменных. Данную функцию необходимо исследовать на экстремум. Для этого должно выполняться необходимое условие существования экстремума:

Найдем частные производные I порядка функции S по переменным a и b:

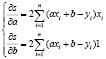
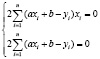
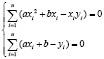
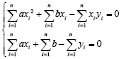
xi – постоянная; a;b – переменные. Следовательно:

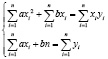
Полученная система уравнений называется системой нормальных уравнений для нахождения значений параметров a и b линейной зависимости 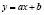, при этом стоит отметить, что чем больше пар чисел, тем точнее будут найдены значения a и b.

Этот метод можно применять для вычисления функций спроса и предложения. Разберем это на примере:

Пусть даны некоторые данные эксперимента:

Согласно этим данным построим кривую спроса:

Определим вид кривой – линейная функция 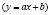. Найдем значения a и b, для этого составим вспомогательную таблицу:

Подставим в следующие формулы получившиеся значения:

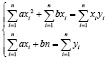
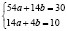
Решим данную систему методом Крамера:

;

;

;

; .

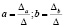
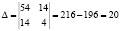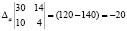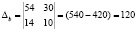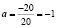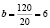Следовательно, уравнение имеет вид: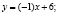

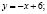
Используя метод наименьших квадратов, определим уравнение кривой предложения:

Данные эксперимента

Согласно данным построим кривую предложения:

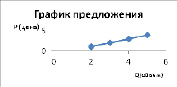
Определим вид кривой – линейная функция 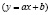. Найдем значения a и b, для этого составим вспомогательную таблицу:

Составим систему уравнений:

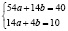
Решим данную систему методом Крамера:

;

;

;

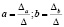
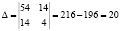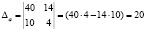
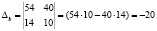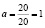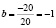
Следовательно, искомое уравнение имеет вид:

; .

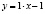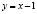Взаимодействие спроса и предложения на определенные товары и услуги устанавливают цену на эти товары и услуги, то есть устанавливается состояние рыночного равновесия. Основными характеристиками такого состояния являются: равновесная цена и равновесный объем. Определить эти значения можно несколькими способами:

– графический, рассмотрим на примере:

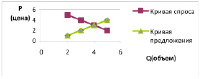
Равновесная цена – 3; равновесный объем – 4.

Математически (используются уравнения кривых спроса и предложения, установленных методом наименьших квадратов):

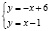
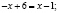
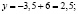
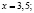
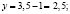
На основании приведенных вычислений можно сделать вывод, что использование математического метода позволяет определить более точные значения равновесной цены и равновесного объема.

В заключениу можно сказать, что мы практически убедились в том, что развитие математики как науки способствует развитию и других наук, в том числе и микроэкономики.

Библиографическая ссылка