Математические методы являются основополагающим механизмом анализа экономических явлений и процессов, направленных на разработку теоретических моделей, позволяющих отразить существующие связи в экономической жизни, прогнозировать поведение экономических субъектов и экономическую динамику. Математическое моделирование становится языком современной экономической теории, одинаково понятным для учёных всех стран мира. Использование методов математической статистики в экономике чрезвычайно широко и различно.
Актуальность изучения статистики вызвана тем, что статистические соображения являются неотъемлемой частью интеллектуального багажа современного человека. Они нужны и для повседневной жизни в современном цивилизованном обществе, и для продолжения образования практически во всех сферах человеческой деятельности, например, таких, как социология, экономика, право, медицина, демография. Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практичных выводов.
В своей статье мы наглядно продемонстрируем возможности математической статистики на примере выдачи кредита в банке.
Одна из функций банков – это выдача кредитов. Человек, взявший кредит, частями возвращает его, а также платит установленный процент за пользование кредитом. В итоге через определенный промежуток времени человек возвращает всю сумму кредита и плату за его использование. Впрочем, существуют некие обстоятельства, некоторые люди не могут реализовать условия кредита. Разумеется, банк может через суд наложить взыскание и тем самым возместить потери. Во всяком случае, для банков более значительным является выдача кредитов, и извлечение из этого максимум прибыли. Таким образом, возникает случайная величина – будет возвращен кредит или нет. Чтобы определить, кому выдать кредит, а кому – нет, банк анализирует статистическую информацию. Сюда относится и кредитная история самого человека, и процент вернувших кредит в срок той категории людей, к которой относится заемщик и тому подобное. Весь этот анализ и исчисляется методами теории вероятностей и математической статистик – вычисление вероятности, вычисление среднего, дисперсии и т.д.
Исходя, из вышеизложенного рассмотрим механизм выдачи кредита в банке на данном примере.
Пример основан на выработки стратегии работы страховых компаний. Наступление или не наступление страхового случая – величина случайная. Страховая компания анализирует статистические данные по наступлению различных страховых случаев и условий, в которых они наступили. Таким образом, можно оценить вероятность наступления страхового случая у страхователя, и в зависимости от ее величины установить для него страховой взнос.
Пусть страховая компания заключает договоры страхования сроком на 1 год на S руб. каждый. Страховой случай происходит с вероятностью p и не происходит с вероятностью q=1–p. Таким образом, имеем закон распределения случайной величины xi– количества страховых случаев у одного (i-го) страхователя (0– если страховой случай не наступил и 1– если наступил):
|
0 |
1 |
|
q |
p |
Легко рассчитать, что
, 
.
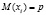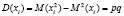Случайная величина
. 
–
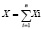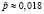количество страховых случаев у страхователей имеет математическое ожидание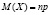 
и дисперсию 
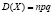. В силу центральной предельной теоремы случайная величина X распределена по нормальному закону. В среднем страховая компания должна будет выплатить npS страховых возмещений. Таким образом, если с каждого страхователя брать по pS руб. страхового взноса (100 p процентов от суммы S), то в среднем у страховой компании будет нулевой баланс. Разумеется, 
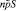страховых возмещений – это величина случайная, и может оказаться как больше (у страховой компании будут убытки), так и меньше (у страховой компании образуется прибыль). Чтобы не было убытков, сумма страхового взноса должна быть больше, чем рассчитано, причем ее величину можно определить с помощью интервальных оценок. Обозначим реальную страховую ставку 
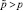. Тогда страховая компания соберет с n страхователей сумму 
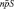рублей. Этой суммы хватит, чтобы возместить потери, связанные с наступлением страхового случая 
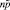клиентам. Обозначим через γ вероятность, что страховая компания не понесет убытков. Тогда вероятность, что количество страховых случаев будет не более, чем, 
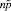есть 
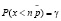. Используя нормальный закон распределения для случайной величины X, имеем:
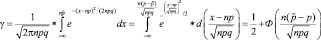
Здесь через Ф обозначена функция Лапласа. Из этого соотношения можно определить страховую ставку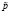 
. Зададим γ= 0,99 (вероятность, что страховая компания не разорится), вероятность наступления страхового случая p = 0,01 и число клиентов n = 1000. Из таблицы со значениями функции Лапласа найдем, что
.
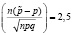Отсюда находим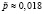 
.
Сделаем вывод: чем больше риск, тем больше будет страховой взнос. Его величина определяется страховой компанией так, чтобы в среднем расходы по наступлению страховых случаев данного типа были меньше, чем доходы в виде страховых взносов от страхователей.
Рассмотрев использование методов математической статистики при решении банковских задач можно сказать следующее, что к экономике математическая статистика применима по той причине, что экономические данные часто представляют собой статистические сведения, т.е. сведения об однородных совокупностях объектов и явлений. Такими однородными совокупностями могут быть выпускаемые промышленностью изделия, персонал промышленности, данные о прибылях предприятий и в нашем случае выдача кредитов в банке.
В современной науке считается, что любая область исследований не может быть настоящей наукой до тех пор, пока в неё не проникнет математика. В этом смысле математическая статистика является полномочным представителем математики в любой другой науке и обеспечивает научный подход к исследованиям. Можно сказать, что научный подход начинается там, где в исследовании появляется математическая статистика. Статистика с необходимостью появляется там, где происходит переход от единичного наблюдения к множественному. Если у вас имеется множество наблюдений, замеров и данных – то без математической статистики вам не обойтись.
Библиографическая ссылка
Абдулхамитова Д.Х., Долгополова А.Ф. ИСПОЛЬЗОВАНИЕ МЕТОДОВ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ ПРИ РЕШЕНИИ БАНКОВСКИХ ЗАДАЧ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 135-136;URL: https://top-technologies.ru/ru/article/view?id=34025 (дата обращения: 22.11.2024).