Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы
• Литература

Хазиев И.Л. 1 Устинова Е.С. 1 Глущенко А.Г. 1 Глущенко Е.П. 1

---

1 Поволжский государственный университет телекоммуникаций и информатики

Статья в формате PDF

1777 KB

1. Глущенко А.Г., Захарченко Е.П. Стимулированная прозрачность запредельных структур с активными параметрами. – Saarbrucken LAP LAMBERT Academic Publishing, 2011. – 186 с.

2. Гринченко В.Т., Вовк И.В., Мацыпура В.Т. Основы акустики. – Киев: Наукова думка, 2007. – 640 с.

3. Осташев В.Е. Распространение звука в движущихся средах. Соврем. проблемы физики. – М.: Наука. Физматлит. 1992г. – 208 с.

4. Глущенко А.Г., Глущенко Е.П., Иванов В.В., Устинова Е.С. Интерференция волн в невзаимных средах. В мире научных открытий.– 2012.– №1.1(25).– С.98-112.

5. Glushchenko A., Glushchenko E., Ivanov V., Ustinova E.. Features of Reflection Acoustic Waves from Mobile Boundary of Section Moving Media. Scientific enquiry in the contemporary world: theoretical basics innovative approach. Titusville, FL, USA, v.1. – p. 6-9.

При отражении волн от подвижных объектов наблюдается изменение частоты (эффект Доплера), отраженных волн по сравнению с частотой падающих на объект волн [1-3]. Для получения формул частоты отраженных волн обычно используются достаточно наглядные геометрические модели. Более детальное исследование с учетом дополнительных условий может быть проведено с помощью волновой теории [4,5]. На практике довольно часто бывают ситуации, когда звуковая волна падает на подвижное препятствие при непостоянной скорости движения границы раздела сред. Исследование особенности такой ситуации проведем на простой модели.

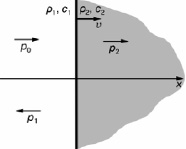
Рис. 1. Пример падающей волны на подвижную границу двух сред

Отражение от равномерно движущейся границы раздела сред. Пусть плоская граница раздела двух сред двигается с постоянной скоростью υ вдоль положительного направления оси Ox (рис.1), причем в момент времени t = 0 ее координата x = 0. Слева от границы расположена акустическая среда с параметрами ρ1, c1, справа – другая среда с параметрами ρ2, c2. На границу слева нормально к ней падает плоская гармоническая волна:

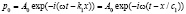. (1)

При взаимодействии волны с границей образуются отраженная волна p1 и прошедшая в другую среду волна p2. Запишем их в виде плоских гармонических волн со своими амплитудами:

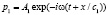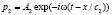, . (2)

Понятно, что p0, p1, p2 удовлетворяют волновому уравнению, но они также должны удовлетворять граничным условиям на подвижной границе, которая изменяет свою координату согласно уравнению x = υt. Итак, граничные условия имеют вид:

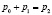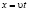, , (3)

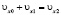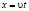, . (4)

Подставим (2) в граничное условие (3):

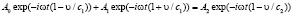. (5)

Данные соотношения должны выполняться для любого момента времени t. Приравнять показатели экспоненты, по аналогии с уравнением:

,

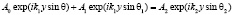где <<fizmat115.wmf>>, нельзя, поскольку очевидно, что 1 – υ/c1 ≠ 1 + υ/c1. Вместе с тем, выбирая амплитуды A1 и A2 можно удовлетворить равенство (5), но только для конкретного момента времени t. Такая ситуация говорит о том, что запись отраженной и прошедшей волн в виде (2) не является правильной. В связи с этим, сделаем предположение: пусть отраженная и прошедшая волны остаются плоскими гармоническими волнами, но их частоты отличаются от частоты ω падающей на границу волны. Итак, запишем волны p1 и p2 в виде:

,

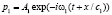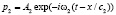. (6)

Представим граничное условие (3) с учетом формул (6) в виде:

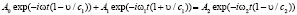(7)

Для выполнения равенства (7) в любой момент времени t необходимо приравнять показатели экспонент:

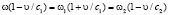. (8)

Отсюда определяем искомые частоты:

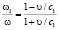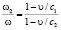, , (9)

Частоты отраженной и прошедшей волн зависят только от соотношения скоростей υ/c1 и υ/c2 . От параметров граничащих сред зависят коэффициенты отражения R= A1/A0 и прохождения T= A2/A0.

Как видим, если граница двигается в направлении распространения волны p0 (скорости υ и c1 по направлению совпадают), то ω1 < ω; если граница двигается навстречу падающей волне (скорости υ и c1 противоположны по направлению).

Из графиков видно, что частота отраженных волн меняется в более широких пределах, чем частота прошедших волн (рис. 3).

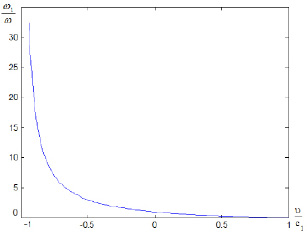
Рис. 2. Зависимость частоты отраженных волн от относительной скорости движения границы раздела сред

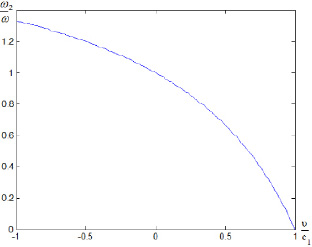
Рис. 3. Зависимость частоты прошедших волн от относительной скорости движения границы раздела сред

Отражение звука от ускоренно движущейся границы раздела сред.

Аналогично, рассматриваем ситуацию, когда звуковая волна падает на подвижное препятствие, только теперь при переменной скорости, в частности, при ускоренном движении с ускорением a. Амплитуды плоской гармонической волны p0, отраженной волны p1 и прошедшей в другую среду волны p2:

, ,

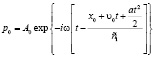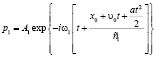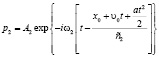. (10)

В данном случае, граничные условия имеют вид:

, ,

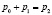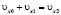при .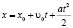

Подставим (10) в граничные условия, взяв x0=0, получим:

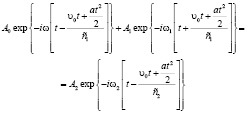
Отсюда соотношение между частотами определяется в виде:

.

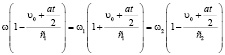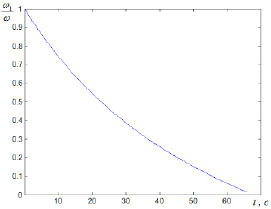
Рис. 4. Зависимость частоты отраженной волны от времени при ускоренном движении границы раздела сред (c=340 м/с, a=10м/с2)

Из рис. 4 видно, что частота отраженного сигнала стремится к нулю при скорости движения границы достигающей скорости распространения волн (отраженный сигнал исчезает, так как волна не догоняет границу раздела сред, не взаимодействует с границей).

Заключение. Рассмотрена волновая теория эффекта Доплера для модели равномерно и ускоренно движущейся плоской границы раздела сред. Частота волн прошедших подвижную границу раздела сред в меньшей степени зависит от скорости движении я по сравнению с частотой отраженных волн.

Библиографическая ссылка