В современном мире во всех сферах происходит процесс интеграции, в котором значительную роль играет экономика. От уровня экономического развития страны зависит степень благосостояния общества, экономическая политика государства и научная деятельность. Поэтому возникла необходимость точно рассчитывать все денежные операции, то есть, нужны математические подсчеты.
Для расчета каждого типа операций существует определенный математический алгоритм, согласно которому и производится вычисление необходимой для выплаты, перечисления, начисления или проведения другой экономической операции суммы. Алгоритм – это последовательность математических, логических или вместе взятых действий, отличающихся детерминированностью, массовостью, направленностью и приводящая к решению задач данного класса за конечное число шагов. Или же, это точное предписание, определяющее последовательность действий, обеспечивающее получение требуемого результата из исходных данных. Таким образом, для любой экономической задачи есть математическое решение.
В данной работе более конкретно будет рассматриваться начисление процентов – задача, установленная для любого современного банка, и актуальная для любого человека, имеющего вклад или кредитную карту.
Целью работы является теоретическое рассмотрение возможности непрерывного начисления процентов. То есть, если рассматривать современные вклады, проценты начисляются либо ежегодно, например, на депозитный счет, либо ежемесячно, например, на сумму, взятую в кредит. В данной работе рассматривается случай, если бы процент начислялся раз в неделю, каждый день, ежечасно, ежесекундно и так далее, стремясь к бесконечно малому числу. Очевидно, что для решения подобной задачи, необходимо обратиться к теории пределов.
Вспомним определение предела: число А называют пределом функции у=f(x) при х→ а, если для любого сколь угодно малого положительного числа E для которого существует такое положительное число ∂ такое, что для любого числа х, удовлетворяющего неравенству |х–а|˂ ∂ будет выполняться неравенство |f(x)–A|˂ E.
Для подсчета процентов необходимо так же обратиться ко второму замечательному пределу. Вторым замечательным пределом (числом е) называется предел числовой последовательности (1+1/n)n при n→±∞.
К числу е приводят решение многих прикладных задач статистики, физики, биологии, химии и др., анализ таких процессов, как рост народонаселения, распад радия, размножение бактерий и пр.
Итак, рассмотрим сначала задачу о ежегодном начислении процентов. Допустим, был открыт депозитный счет на k лет, и первоначальный вклад в банк составил X0 денежных единиц. Ежегодно банк выплачивает p % годовых. Необходимо найти Хn, то есть размер вклада через k лет.
Проценты делятся на два вида: простые и сложные. При использовании простых процентов размер вклада будет ежегодно увеличиваться на одну и ту же величину pX0/100. Таким образом, сумма вклада через 1 год будет равняться X0(1+р/100), через 2 года – X0(1+2р/100), и мы получим следующий ответ к задаче:
Xk=X0(1+рk/100).
Однако на практике в преимущественном большинстве применяются сложные проценты. В отличии от простых процентов, вклад ежегодно будет увеличиваться не на одно и то же число, а в одно и то же (1+р/100) число раз, то есть:
X1=X0(1+р/100), X2=X0(1+р/100)2 и так далее, следовательно, ответом будет являться:
Xk=X0(1+р/100)k.
Теперь же перейдем непосредственно к задаче о непрерывном начислении процентов. Если начислять проценты по вкладам не один раз в году, а n число раз, то при том же ежегодном приросте р % процент начисления составит за 1/n-ю часть года р/n %, а размер вклада за k лет при kn начислениях будет равен:
Xk=X0(1+p/100n)kn.
Предположим, что проценты по вкладу начисляются каждое полугодие (n=2), ежеквартально (n=4), ежемесячно (n=12), каждый день (n=365), каждый час (n=8760) и так далее, при n→∞, то есть, непрерывно. Тогда задача будет иметь следующее решение:
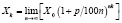 .
.
Можно заметить, что полученная формула напоминает вид второго замечательного предела, о котором упоминалось выше, необходимо лишь дополнить имеющееся уравнение. По свойству пределов вынесем X0 за знак предела, так как X0 является числом, а предел константы равен самой константе. Оставшуюся скобку возведем в степень, обратную дроби p/100n, с целью перехода ко второму замечательному пределу, и домножим оставшуюся степень nk на p/100n с целью сохранения знака равенства:
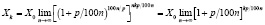 .
.
Теперь мы получаем следующий ответ к задаче:
Xk=X0 epk/100, где рk/100 – ставка непрерывных процентов – является силой роста
Рассмотрим применение полученных формул для решения более конкретной задачи, чтобы выделить разницу в результатах в зависимости от способа начисления процентов.
Возьмем X0=1 денежной единице, p=5 %, k=20 лет.
Первый способ:
Начисление простых процентов
Xk=X0(1+рk/100).
Xk=1(1+5·20/100)=2,0000.
Второй способ:
Начисление сложных процентов
Xk=X0(1+р/100n)kn
1)n=1
Xk=1(1+5/100·1)1·20=2,6355
2)n=2
Xk=1(1+5/100·2)2·20=2,6851
3)n=4
Xk=(1+5/100·4)3·20=2,7015
4)n=12
Xk=(1+5/100·12)12·20=2,7126
5)n=365
Xk=(1+5/100·365)365·20=2,7181
Третий способ:
Начисление непрерывных процентов
Xk=X0 epk/100
Xk=1·2,7182…5·20/100=е=2,7182
Таким образом, становится очевидно, что погрешность вычисления вклада по формуле непрерывного начисления процентов по сравнению с результатом по формуле сложных процентов, начисляемых ежегодно (n=1), оказалась незначительной, но заметной – около 0,08, в то время как разница между результатом непрерывного начисления и простых процентов равна практически 0,7.
В практических финансово-кредитных операциях крайне редко используются непрерывное начисление процентов, с теоретической точки зрения оно оказывается весьма эффективным, например, при анализе сложных финансовых проблем, таких как обоснование и выбор инвестиционных решений.
В экономике метод математического моделирования сильно развит, так как он помогает взглянуть на упрощенную ситуацию, получить идеальную модель, в данном случае, начисления процентов и сравнить ее с реальной ситуацией, таким образом выявив недостатки существующей системы и, возможно, найти способ их устранения.
В данной работе описан именно такой пример, ведь, если бы не математическое решение и анализ, то разницу между начислением простых и сложных процентов выявить было бы невозможно, а значит, экономика теряла бы средства за счет значительных погрешностей в расчетах.
Из всего вышесказанного можно сделать вывод о том, что непрерывное начисление процентов на практике практически не применимо, однако именно с его помощью осуществляется возможность анализа финансовой ситуации различных коммерческих предприятий, появляются новые цели и задачи развития.
Библиографическая ссылка
Рыбачева И.А., Нуйкина Е.Ю. НЕПРЕРЫВНОЕ НАЧИСЛЕНИЕ ПРОЦЕНТОВ В ФИНАНСОВОЙ МАТЕМАТИКЕ // Современные наукоемкие технологии. 2014. № 5-2. С. 121-122;URL: https://top-technologies.ru/ru/article/view?id=34016 (дата обращения: 05.03.2026).



