При рассмотрении наземных локомоций «ходьба» и «бег», с точки зрения биомеханики, возникает парадокс. Для бега характерен, в целом, тот же цикл движений, что и при ходьбе, те же действующие силы и функциональные группы мышц, что и при ходьбе и его можно рассматривать как предельный случай. Отличие заключается в наличии при беге так называемой «фазы полета», когда обе ноги человека не касаются земли [1]. Интуитивно возникает впечатление, что при беге положение человека в пространстве менее устойчиво, с другой стороны опыты показывают, что при увеличении скорости ходьбы и переходе на бег положение человека в пространстве становится более устойчивым.
В ходе исследования было проведено математическое моделирование. Нами был выбран простой физический аналог – математический маятник с точкой подвеса в области голеностопных суставов. Процесс ходьбы моделировался как вибрация точки подвеса, т.к. частота колебаний подвеса велика по сравнению с частотой колебаний маятника.
Такой маятник впервые был исследован еще в 1908 г. А. Стефенсоном [2]. Теоретическая модель маятника с вибрирующей точкой подвеса была построена академиком и нобелевским лауреатом П.Л. Капицей [3].
На рисунке изображена графическая модель Маятника Капицы.
Математическая модель задается уравнением, описывающим данную систему:
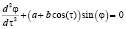, (1)
где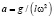 
; 
.
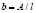По своему смыслу – отношение квадрата собственной частоты маятника к квадрату частоты колебаний подвеса (отношение квадрата собственной частоты маятника к темпу ходьбы), – отношение амплитуды колебаний подвеса к длине маятника (отношение длины шага к расстоянию от голеностопного сустава до центра масс).
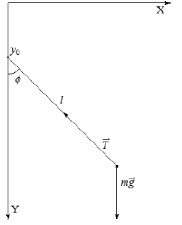
Математический маятник с вибрирующей точкой подвеса. (y0 – точка подвеса; l – расстояние от ОЦМ(общего центра масс) до голеностопного сустава;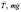 
– силы, действующие а ОЦМ; f – отклонение от положения равновесия)
Результаты моделирования показали, что, несмотря на простоту, выбранная модель является адекватной, т.к. наблюдается следующая зависимость – чем меньше задаваемое значение , то есть чем выше темп ходьбы, тем устойчивее равновесие маятника. Причем эта устойчивость достигается в верхнем положении, что соответствует выбранной изначально модели с точкой подвеса в области голеностопных суставов и материальной точкой в области центра масс человека (перевернутый маятник).
С помощью математического пакета была построена визуализация компьютерного эксперимента, позволяющая динамически менять параметры, и воспроизводить результаты математического моделирования.
Библиографическая ссылка
Ракитова Ю.М., Сивашова Е.С. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НАЗЕМНОЙ ЛОКОМОЦИИ «ХОДЬБА» С ПОМОЩЬЮ МАЯТНИКА КАПИЦЫ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 120-121;URL: https://top-technologies.ru/ru/article/view?id=34015 (дата обращения: 25.04.2024).