При создании и проектировании гиперзвукового летательного аппарата различного назначения необходимо детальное значение их аэротермодинамических характеристик вдоль всей траектории полета. В процессе исследования тепловых нагрузок, действующих на поверхность космических аппаратов, важным этапом является решение задачи создания их тепловой защиты и определения температурных режимов конструкции. В настоящее время существует несколько подходов решения аэротермодинамических характеристик гиперзвуковых летательных аппаратов, также проведены многочисленные исследования аэродинамических характеристик космических аппаратов вдоль всей траектории – от орбитального полета до посадочного режима [1-3]. Однако обладают достаточно хорошей точностью, но требуют большого времени для вычисления. Другие основы на упрошенных инженерных методиках требуют малых затрат расчетного времени, но специфика существующих алгоритмов быстрого счёта позволяет оценивать тепловые потоки на телах достаточно простой формы.
Для вычисления коэффициента теплопередачи Ch на элементарную площадку в свободномолекулярном пределе используются аналитические формулы в виде [4]:
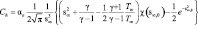 ,
,
где
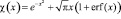 ,
,
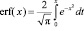 ,
,
αe – коэффициент аккомодации энергии на стенке, s∝ – отношение скорости набегающего потока к наиболее вероятной скорости молекул, Tw – температура стенки, T∝ – температура набегающего потока, g – показатель адиабаты, s∝,q = s∝ cos q.
В случае же континуального режима обтекания для вычисления коэффициента теплопередачи необходимо учитывать изменение параметров потока при движении вдоль поверхности.
Для вычисления коэффициента теплопередачи Ch в континуальном режиме будем использовать методику, основанную на теории Лиса [5].
Коэффициент теплопередачи в произвольной точке тела вычисляется по формуле
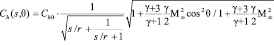 .
.
Здесь s – расстояние вдоль линии тока от точки торможения до рассматриваемой элементарной площадки, q – угол между направлением потока и нормалью к элементарной площадке в данной точке, Ch0 – коэффициент теплопередачи в точке торможения:
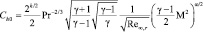 .
.
Здесь k = 1 для сферической точки торможения, k = 0 для цилиндрической точки торможения, r – радиус кривизны поверхности в точке торможения, w – показатель степени в степенной зависимости вязкости от температуры, Pr = mCp/c – число Прандтля, число Рейнольдса Re∝,r вычислено по параметрам набегающего потока и радиусу кривизны в точке торможения. Число Рейнольдса в континуальном и около континуальном режимах, так как при приближении к свободномолекулярному режиму, когда Re → 0, величина Ch0 → 0.
В настоящей работе предлагается локально-мостовой метод вычисления коэффициента теплопередачи на элементах выпуклой поверхности с учетом расстояния от точки торможения в переходном режиме. Локально-мостовой метод позволяет быстро получить аэротермодинамические характеристики при проведении большого количества многовариантных расчетов [6]:
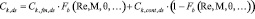 ,
,
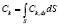 .
.
Здесь M – число Маха, Re – число Рейнольдса, S – площадь поверхности тела. Функция Fb называется мостовой функцией. Рассмотрим мостовую функцию, выражающуюся как функция ошибки от логарифма числа Кнудсена:
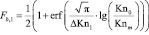 ,
,
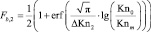 .
.
Если Kn0 < Knm, используется мостовая функция Fb,1. В противном случае Fb,2. Значения Knm = 0.3, ΔKn1 = 1.3 и ΔKn2 = 1.4 были определены путем сравнения с результатами моделирования методом прямого статистического моделирования (Монте-Карло). Разработанная методика для расчета тепловых потоков на тело имеет практический интерес для организации и специалистов, занимающихся определением теплового потока.
На рисунке показаны зависимости коэффициента теплопередачи на сфере от угла при различных числах Рейнольдса (Re = 0.1, 3.8, 3243). Полученные результаты сравнены с результатами Dogra V.K., Wilmoth R.G. [7] и Ващенкова П.В. [6]. Здесь угол откладывается от точки торможения.
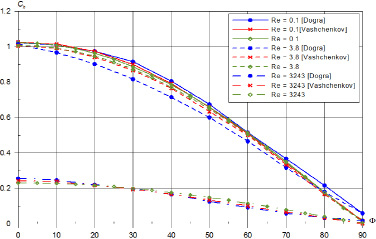
Угловое распределение Ch на сфере
На рисунке видно, что тепловой поток в свободномолекулярном и в континуальном режимах локально-мостовым методом определяется хорошо, но в переходном режиме дает повышенное значение коэффициента примерно на 15 % на углах 20–55 градусов [6, 10]. Можно сказать, что результаты, полученные локально-мостовым методом, дают правильное поведение и достаточно хорошо согласуются с результатами метода прямого статистического моделирования (ПСМ). Локально-мостовой метод дает в переходном режиме завышенное значение коэффициента теплопередачи примерно на 15 % на углах 20–50 градусов. Методики и результаты смогут быть полезны при создании современных и перспективных воздушно-космических аппаратов нового поколения [8-11]. Работа выполнена при поддержке РФФИ (Грант № 14-07-00564-а).
Библиографическая ссылка
Зея Мьо Мьинт МЕТОДИКА ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ КОЭФФИЦИЕНТА ТЕПЛОПЕРЕДАЧИ НА ТЕЛАХ СЛОЖНОЙ ФОРМЫ В ПЕРЕХОДНОМ РЕЖИМЕ // Современные наукоемкие технологии. 2014. № 5-2. С. 115-116;URL: https://top-technologies.ru/ru/article/view?id=34011 (дата обращения: 05.03.2026).



