Развитие ракетно-космической техники требует непрерывного совершенствования науки о процессах теплообмена, развития теории теплопередачи [1-6]. В настоящее время существует несколько подходов к оценке конвективного теплообмена сверхзвуковых летательных аппаратов. Они обладают достаточно хорошей точностью, но требует большого времени для вычисления. Другие основаны на упрощенных инженерных методиках, требуют малых затрат расчётного времени, но специфика существующих алгоритмов быстрого счёта позволяет оценивать тепловые потоки на телах простой формы. Одним из таких методов является метод эффективной длины [2, 3, 7].
Этот метод основан на использование особенностей развития пограничного слоя, заключающихся в том, что в случае ускоренных течений теплообмен в рассматриваемом сечении определяется в основном параметрами потока и толщиной пограничного слоя в этом сечении. В значительно меньшей степени тепловой поток зависит от условий, в которых пограничный слой развивался от точки его образования до рассматриваемого сечения. В соответствии с этими особенностями, метод эффективной длины состоит в том, что при расчете теплообмена действительное сечение заменяется течением над пластиной (для осесимметричного тела – над цилиндром) с параметрами потока, равными параметрам рассматриваемого сечения. Длина пластины или цилиндра xэф выбирается из условия нарастания на ней теплового пограничного слоя толщиной, равной толщине слоя в рассчитываемого сечения тела.
Целью настоящей работы является определение конвективного теплообмена на поверхности тела при ламинарном и турбулентном пограничном слое с использованием метода эффективной длины.
Формулы для расчета теплообмена при ламинарном пограничном слое
Тепловой поток определяется по формуле Ньютона
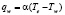
где
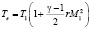 .
.
Для воздуха при ламинарном пограничном слое r = 0.84.
Критериальное уравнение для определения коэффициента теплоотдачи при течении над пластиной
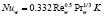 .
.
Коэффициент K учитывает влияние сжимаемости. Используя это уравнение и метод эффективной длины для расчета теплообмена при произвольном распределении параметров потока вдоль образующей тела, будем иметь
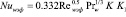
где K1 – поправка на влияние продольного градиента давления
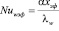 ,
, 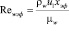
В частном случае Tw = const, приближенное выражение для определения эффективной длины имеет вид
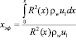
Под интегралом стоят переменные величины R(x), ρw, u1 изменяющиеся от начала образования пограничного слоя (критическая точка) до рассматриваемого сечения. В знаменателе R(x), ρw, u1 соответственно радиус вращения, плотность и скорость в рассматриваемом сечении.
Учитывая постоянство Tw, плотность газа ρw можно определить из соотношения
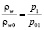
где ρw0 и p01 параметры воздуха в критической точке.
Поправка на сжимаемость рассчитывается по формуле
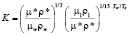 ,
,
где µw и ρw определяются по Tw, µ1, ρ1 по T1, а m*r* по максимальной температуре Tmax = T* в пограничном слое.
При 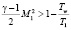
T* определяется по формуле
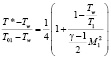 .
.
При 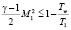
Максимальная температура в пограничном слое равна температуре внешнего потока T* = T1. В этом случае
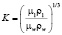 .
.
Поправка на влияние градиента скорости
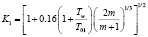
где m – показатель степени в выражении u1 = b xm,
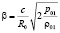 ,
, 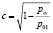 .
.
При течении в окрестности критической точки m = 1 и
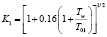 .
.
В случае обтекания конуса m = 0, K1 = 1.
Определив критерий Нуссельта Nuwэф и можно найти коэффициент теплоотдачи
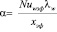 .
.
Формулы для расчета теплообмена при турбулентном пограничном слое
Тепловой поток определяется по формуле Ньютона. Эффективная температура имеет вид
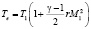 .
.
где r = 0.89.
Критериальное уравнение для определения коэффициент теплоотдачи методом эффективной длины имеет вид
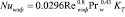
KT – поправка на сжимаемость. Здесь
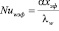 ,
, 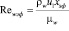
Эффективная длина пластины при турбулентном течении в пограничном слое и Tw = const определится из выражения
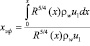 .
.
Из формулы получено в предположении постоянства по x выражения –
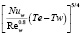 .
.
В окрестности критической точки изменение этих величин невелико и переменностью их по x можно пренебречь.
Где скорость потока невелика, хорошие результаты дает поправка на сжимаемость, определенная как
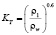 .
.
При большой скорости потока
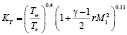 .
.
Коэффициент теплоотдачи
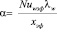 .
.
В отдельных случаях при технических расчетах для определения коэффициента теплоотдачи удобнее пользоваться критериальным уравнением, в котором определяющей температурой является температура потока на внешней границе пограничного слоя. Для большой скорости потока такое уравнение имеет вид
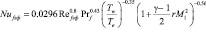
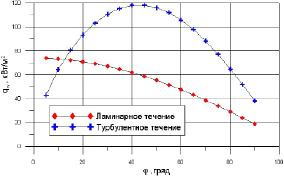
Распределение тепловых потоков на сфере
Работа выполнена при поддержке РФФИ (Грант № 14-07-00564-а).
Библиографическая ссылка
Зея Мьо Мьинт, Хлопков А.Ю. МЕТОДИКА РАСЧЁТА КОНВЕКТИВНЫХ ТЕПЛОВЫХ ПОТОКОВ НА ПОВЕРХНОСТИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ В ПОГРАНИЧНОМ СЛОЕ // Современные наукоемкие технологии. 2014. № 5-2. С. 113-115;URL: https://top-technologies.ru/ru/article/view?id=34010 (дата обращения: 05.03.2026).



