Из-за действия шумов, ограниченности полосы пропускания тракта магнитной записи-воспроизведения (МЗВ) и других причин форма воспроизводимых сигналов может существенно отличаться от записываемых.
Целью коррекции и детектирования является «очищение» воспроизводимого цифрового сигнала от помех и придание ему вида, пригодного для декодирования. При высокой плотности записи ограниченность АЧХ тракта МЗВ в области верхних частот приводит к взаимному воздействию воспроизводимых импульсов, которое называют межсимвольной интерференцией (МСИ) [1].
Методы детектирования воспроизводимых импульсов можно разбить на две группы:
а) поэлементное детектирование, при котором решение 0 это или 1 принимается на основе последовательного анализа каждого воспроизводимого символа;
б) детектирование по алгоритму Витерби, при котором решение 0 это или 1 принимается в результате анализа группы воспроизводимых символов.
Амплитудный и другие методы поэлементного детектирования достаточно подробно описаны в литературе.
Рассмотрим некоторые аспекты парциального детектирования по алгоритму Витерби, которое применяется в цифровых системах форматов Digital Betacam, MPEG IMX (D10) [2].
Для примера рассмотрим систему PR4, в которой отсчеты имеют только три уровня {–1,0,1} и предположим, что в канале воспроизведения действует аддитивная смесь сигнала S(t) и Гауссовского шума N(t). При поэлементном амплитудном детектировании происходит последовательное сравнение воспроизводимых отсчетов Uk(t)=Sk(t)+Nk(t) с пороговыми уровнями ±0,5:
если Uk(t)>0,5, то отсчет равен 1,
если Uk(t)<–0,5, то отсчет равен -1,
если Uk(t) ≤ 0,5, то отсчет равен 0.
Предположим, что на вход детектора поступает следующая последовательность зашумленных отсчетов: 0,3, –0,6, –0,4, 0,7,0,9, 1,2, 0,2.
В соответствии с алгоритмом работы порогового детектора на его выходе будет последовательность Sk = 0, –1, 0, 1, 1, 1, 0.
Каждый класс сигналов PR имеет вполне определенные значения отсчетов. Из переходной и импульсной характеристик PR4 следует, что в системах PR4 не могут быть подряд три «единицы» [4]. Однако у поэлементного порогового детектора нет памяти, он ничего «не знает» о предыдущих и последующих отсчетах, он принимает решение 0 это или 1 по каждому отдельному отсчету.
Таким образом, три подряд 1 – это ошибочная комбинация: после двух 1 должен быть 0 или -1. Нетрудно предложить несколько близких к Sk последовательностей (табл. 1).
Таблица 1
|
Отсчеты Sk |
0,3 |
-0,6 |
-0,4 |
0,7 |
0,9 |
1,2 |
0,2 |
|
Последовательность N1 |
0 |
-1 |
0 |
1 |
1 |
0 |
0 |
|
Последовательность N2 |
0 |
-1 |
0 |
0 |
1 |
1 |
0 |
|
Последовательность N3 |
0 |
-1 |
0 |
0 |
0 |
1 |
1 |
Анализируя табл. 1, определим насколько последовательности N1, N2, N3 соответствуют воспроизводимым отсчетам. Последовательность N1 имеет отсчеты 0,7 и 0,9 соответствующие 1 (это правдоподобно), однако отсчету 1,2 соответствует 0, что маловероятно. Последовательность N2 имеет отсчет 0,7, соответствующий 0, это сомнительно, в то же время 0,9 и 1,2 соответствуют 1, что правдоподобно. В последовательности N3 отсчеты 0,7 и 1,2 соответствуют 0 (весьма неправдоподобно), а отсчет 1,1 соответствует 1 (это правдоподобно). Из анализа следует, что наиболее правдоподобным результатом детектирования следует считать последовательность N2. Количественную оценку этого можно получить путем вычисления среднеквадратичного расстояния (Mean-Squared Distance – MSD) между отсчетами и возможными комбинациями последовательностей (1)
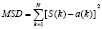 , (1)
, (1)
Вычисления по формуле (1) дают следующие результаты: последовательность N1 – MSD= 2,35, последовательность N2 – MSD=0,99, последовательность N3 – MSD=2,48. Таким образом, последовательность N2 максимально правдоподобна воспроизводимым отсчетам.
Рассмотренный пример иллюстрирует принцип работы детектора Витерби:
– в отличие от поэлементного детектора решение принимается в результате анализа последовательности воспроизводимых отсчетов;
– для каждой последовательности воспроизводимых отсчетов создается возможный набор допустимых продетектированных последовательностей;
– каждая допустимая последовательность сравнивается с воспроизводимыми отсчетами и вычисляется MSD;
– последовательность с минимальным MSD (максимально-правдоподобная) считается результатом детектирования.
Количественная оценка эффективности применения детектора Витерби в канале цифровой магнитной записи c аддитивным Гауссовским шумом дана в [3, 5].
Используя результаты этих работ, рассчитаны вероятности битовой ошибки BER (Bit Error Rate) для канала PR4 в зависимости от SNR (Signal to Noise Ratio – отношениe сигнал/шум) (рис. 1): кривая (тонкая) соответствует максимально правдоподобному детектору по алгоритму Витерби, а кривая (жирная) – амплитудному пороговому детектору.
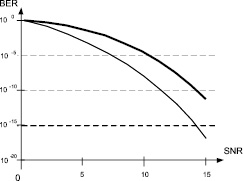
Вероятность битовой ошибки в зависимости от отношения сигнал/шум
Из рисунка видно, что детектор Витерби позволяет уменьшить вероятность ошибки на 1-2 порядка (зависит от SNR) по сравнению с амплитудным детектором[4]. Комбинацию системы PR определенного класса с максимально правдоподобным детектором (Maximum Likelihood Detector) принято называть сокращенно PRML (Partial Response Maximum Likelihood) – канало мили системой PRML. Технология PRML существенно повышает энергетическую эффективность и эффективность использования полосы частот канала записи-воспроизведения [3, 5]. Мерой увеличения энергетической эффективности PRML в сравнении с амплитудным детектором является величина, показывающая, насколько можно снизить отношение сигнал/шум, чтобы обеспечить заданную достоверность записи-воспроизведения, определяемую вероятностью битовой ошибки. Например, система PR4 обеспечивает такую же вероятность битовой ошибки, как амплитудный детектор при меньшем на 3 дБ отношении сигнал/шум (табл. 2).
Таблица 2
Эффективность PRML по сравнению с амплитудным детектором
|
Система PRML |
Энергетический выигрыш |
Плотность записи |
|
PR4 |
1,41 (3 Дб) |
1,1 |
|
EPR4 |
2 (6 Дб) |
1,33 |
|
E2PR4 |
3,16 (10 Дб) |
1,54 |
Мерой улучшения эффективности использования полосы частот системы PRML по сравнению с амплитудным детектором является выигрыш в плотности записи (табл. 2.) Практически энергетический выигрыш и выигрыш в плотности записи несколько меньше, чем приведенный в табл. 2, так как при теоретическом анализе не учитывались ошибки синхронизации, нелинейные искажения, не идеальность формирования сигналов PR и ряд других факторов.
Библиографическая ссылка
Албутова Е.В., Шмокин М.Н. ДЕТЕКТИРОВАНИЕ И КОРРЕКЦИЯ ЦИФРОВЫХ СИГНАЛОВ ДЛЯ УСТРОЙСТВ МАГНИТНОЙ ЗАПИСИ С МАКСИМАЛЬНЫМ ПРАВДОПОДОБИЕМ // Современные наукоемкие технологии. 2014. № 5-2. С. 84-86;URL: https://top-technologies.ru/ru/article/view?id=33971 (дата обращения: 05.03.2026).



