Был произведен предварительный расчет составной деревянной балки, состоящей из двух брусьев, соединенных между собой с помощью механических податливых связей- металлических зубчатых пластин. Податливостью называется способность связей при деформировании элементов давать возможность соединяемым брусьям сдвинуться относительно друг друга.
Податливость связей ухудшает работу составных элементов по сравнению с элементами цельного сечения. У составного элемента на податливых связях снижается прочность и увеличивается деформативность. Поэтому при расчете и проектировании таких элементов необходимо учитывать податливость связей.
В изгибаемых элементах составного сечения податливые связи препятствуют сдвигу отдельных соединяемых слоев относительно друг друга (рис.1).
Расчет составного элемента на податливых связях при поперечном изгибе сводится к расчету изгибаемого элемента цельного сечения с введением понижающих коэффициентов (kW
1) и (kЖ
1), учитывающих податливость связей.
Исходные данные:
Дана деревянная балка составного сечения, состоящая из двух брусьев из древесины сосны 2 сорта, соединенных между собой металлическими зубчатыми пластинами (рис.1). Пролет балки l=6м, h=29.2 cм, на балку действует распределенная нагрузка q=300кгс/м.
Задание:
Рассчитать балку, определить геометрические размеры поперечного сечения, определить площадь металлических зубчатых пластин.
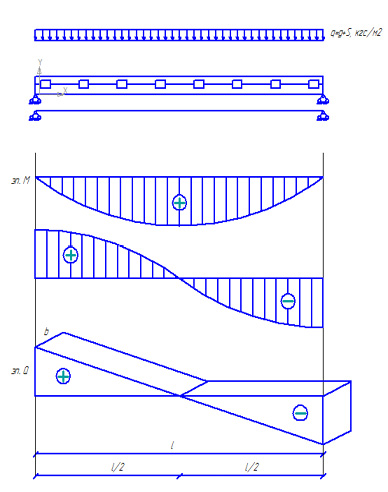
Рис.1 Поперечный изгиб деревянной составной балки на МЗП, пролетом l=6м.
Из формулы расчета на прочность по скалыванию древесины находим величину касательных напряжений по п.6.10 [3].
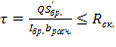кгс/м2 (1)
Где Q- расчетная поперечная сила, находится по формуле:
Q=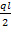
, кгс (2)
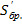- статический момент брутто сдвигаемой части сечения относительно нейтральной оси для прямоугольного сечения:
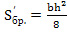, м3 (3)
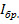момент инерции брутто поперечного сечения элемента относительно нейтральной оси:
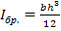, м4 (4)
bрас.- расчетная ширина сечения элемента, м
Rск.- расчетное сопротивление скалыванию при изгибе, МПа.
Исходя из формул 1-4, получаем:
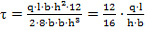, кгс/м2
Вычисляем сдвигающее усилие на опоре по формуле:
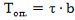, кгс (5)
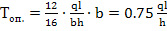, кгс
Находим суммарное сдвигающее усилие по формуле:
=
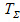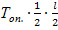, кгс (6)
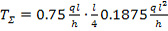, кгс
Подставляем все известные данные в формулу и получаем:
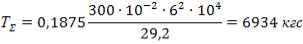
Находим расчетную площадь металлических зубчатых пластин на участке с однозначной эпюрой Q:
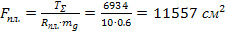(7)
Принимаем bпл=14,2 см, lпл.=81,4 см, а коэффициент податливости mg принимаем равный 0.6. Располагаем пластины с двух сторон: 4 пластины размером 142х200 мм. Учитывая, что коэффициент mg взят из методики расчета узловых соединений, а в балках он может быть существенно меньше, условно принимаем его равным 0.5.
Принимаем bпл=14,2 см, lпл.=100 см, а коэффициент податливости mg для балки вычислим из формулы (7):
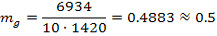
Найдем высоту составной балки по формуле:
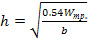, см (8)
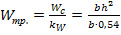(9)
b=46 мм
Wтр.- момент сопротивления составной балки с учетом понижающего коэффициента kw
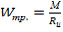, м3 (10)
Где М- изгибающий момент, вычисляемый по формуле:
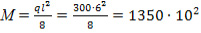кг
см (11)
Где q=300 кгс/с- нагрузка, действующая на балку,
l=6 м- пролет балки,
Rи=130 кгс/см2 расчетное сопротивление изгибу древесины сосны 2 сорта,
Подставляем данные в формулу (10) и получаем:
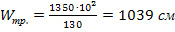3
Находим высоту поперечного сечения составной балки
H=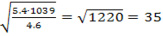
см.
Выбираем 2 доски высотой 196 и 146 мм каждая (см. рис.1). Общая высота балки равна 342мм.
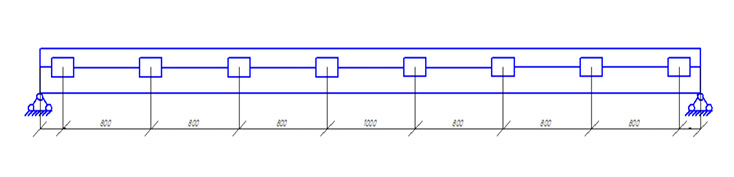
Рис. 2 Расстановка МЗП.
Библиографическая ссылка
Логинова К.В., Миронов В.Г. РЕЗУЛЬТАТЫ РАСЧЕТА СОСТАВНОЙ БАЛКИ НА МЕТАЛЛИЧЕСКИХ ЗУБЧАТЫХ ПЛАСТИНАХ // Современные наукоемкие технологии. – 2014. – № 5-1. – С. 155-157;URL: https://top-technologies.ru/ru/article/view?id=33792 (дата обращения: 21.11.2024).