Понятие о КИН вводят в процессе решения бигармонического уравнения
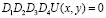(1)
при заданных граничных условиях на поверхности трещины [1]. Например, КИН KI (случай нормального отрыва берегов трещины) определяется формулой
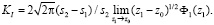(2)
Здесь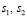 
зависят от упругих характеристик материала; z1 – комплексная переменная; 
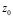соответствует острию трещины; 
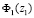– функция Гурса [1]. КИН зависят от геометрий тела и трещины, от внешних нагрузок. В общем случае задача определения КИН представляет собой непростую математическую проблему. Целью настоящей работы является упрощение задачи определения КИН и критериев разрушения при изменении ориентации трещин. Для достижения этой цели используются математические методы.
Основные результаты. КИН являются физическими величинами, не зависящими от выбора системы координат. Математически такие объекты представляются тензорами [2]. Пусть в системе координат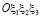 
компоненты тензора КИН определены:
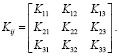(3)
Здесь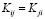 
. На рис. 1 указаны положительные направления Kij. Индекс i у Kij соответствует оси ξi, параллельно которой направлен Kij; индекс j соответствует оси ξj, перпендикулярной берегам рассматриваемой трещины. Направления КИН на рис. 1 соответствуют направлениям сил, стремящихся деформировать берега трещины (в общем случае анизотропных и композитных тел при «действии» только K11, например, происходит не только раскрытие берегов соответствующей трещины, но и их сдвиги). При переходе от системы координат 
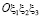к системе 
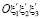путем поворота вокруг точки O компоненты тензора Kpq преобразуются по следующей формуле [2]:
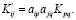(4)
Здесь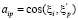 
; 
.
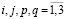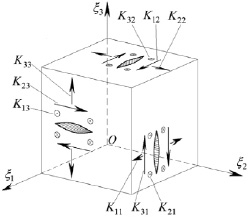
Рис. 1. Положительные направления КИН Kij,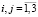 
. 
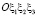– принятая система координат
Тензор КИН (3) характеризует концентрацию напряжений в окрестности точки А тела, где три ортогональные трещины имеют общую вершину (рис. 2). Если компоненты Kij в некоторой системе координат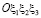 
определены в результате решения соответствующей задачи математической теории упругости, то есть уравнения (1) при заданных граничных условиях, то формулы (4) позволяют сравнительно легко определять компоненты 
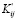для той же совокупности трещин, повернутых относительно своего первоначального положения. При этом остальные исходные условия рассматриваемой задачи сохраняются (взаимная ортогональность трещин, длины их профилей, внешние нагрузки на тело и т.п.).
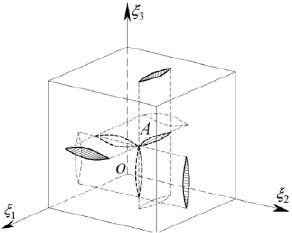
Рис. 2. Точка А является общей вершиной трех ортогональных трещин
Отметим, что суперпозиция решений, полученных для точки А отдельных трещин (рис. 2) допустима, так как для определения КИН используют соотношения линейной механики разрушения [3].
Рассмотрим случай, когда поворот системы координат происходит на угол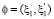 
. Тогда формулы (4) принимают следующий вид:
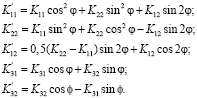(5)
Для задачи о наклонной трещине, расположенной в поле одноосных растягивающих напряжений, формулы (5) дают те же результаты, которые приведены в [1, c. 109].
Критерии разрушения определяют условие начала роста макротрещины. Нами принято, что характеристики трещиностойкости материала не следуют из других его характеристик (таких, как пределы прочности и т п.). Поэтому необходимо применять так называемые «эмпирические» критерии разрушения [3]. Примем следующие обозначения:
.
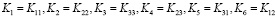Допустим, что критерий разрушения можно записать в виде уравнения второй степени:
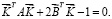(6)
Здесь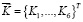 
; компоненты симметрической матрицы А и вектора 
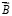подлежат экспериментальному определению. Индекс Т означает транспонирование.
Рассмотрим комбинацию плоской и антиплоской задач анизотропной теории упругости и сквозную трещину с профилем в плоскости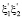 
. Анизотропное тело в каждой своей точке имеет плоскость упругой симметрии, перпендикулярную оси 
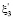[1]. Пусть для рассматриваемого случая известен следующий эмпирический критерий разрушения:
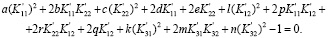(7)
Переход к системе координат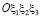 
с использованием (5) преобразует (7) к виду:
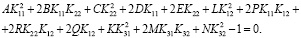(8)
Здесь
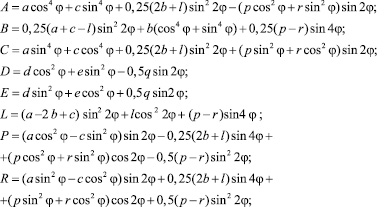(9)
Как видно из приведенных выше результатов, критерии разрушения при повороте трещин преобразуются так же, как и критерии прочности, записанные в пространстве напряжений, при повороте соответствующей системы координат.
Пример расчета. В качестве примера рассмотрим пластину из однонаправлено армированного стеклопластика со сквозной трещиной, ориентированной параллельно волокнам. В работе [4] для этого материала приведены следующие характеристики трещиностойкости:
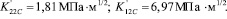(10)
Дополнительно к (10) примем еще две предельные точки в плоскости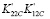 
:
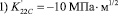, остальные КИН=0; (11)
, 
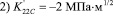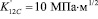, остальные КИН=0.
Уравнение эллипса в плоскости переменных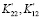 
:
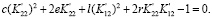(12)
Подставляя (10) и (11) в (12), находим:
; 
;
; 
.
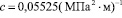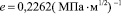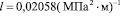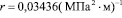Для случая j=45° согласно (9) имеем:
; 
;
; 
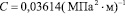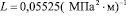
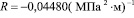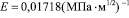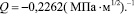
Уравнение соответствующего сечения поверхности (8):
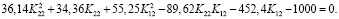(13)
Эллипс (13) имеет следующие точки пересечения с осями координат:
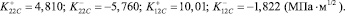(14)
Полученные результаты (14) качественно правильно отражают рассматриваемое явление. Когда трещина наклонена под углом (–45°) к армирующим волокнам (то есть j=45°), некоторые характеристики трещиностойкости увеличиваются, а некоторые – уменьшаются (по модулю) по сравнению с соответствующими характеристиками, когда этот угол равен нулю (например,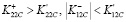 
). Для количественной оценки полученных результатов необходимо провести соответствующие эксперименты.
Заключение
Между тензорами КИН Kij и напряжений σij имеется большая аналогия. У них даже размерности близки друг другу (МПа·м1/2 и МПа соответственно). По аналогии с исследованием напряженного состояния в точке тела [5], можно исследовать КИН – состояние в окрестности рассматриваемой точки. Особое значение имеет, на наш взгляд, возможность записи критериев разрушения для различных ориентаций трещин в анизотропных и композитных телах, применяя формулы вида (4), (5) и исходные эмпирические критерии разрушения для начальной ориентации трещин. Учет тензорного характера КИН может существенно сократить объемы необходимых теоретических и экспериментальных исследований в механике трещин.
Библиографическая ссылка
Сибгатуллин Э.С., Сибгатуллин К.Э. О ТЕНЗОРЕ КОЭФФИЦИЕНТОВ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ И КРИТЕРИЯХ РАЗРУШЕНИЯ В МЕХАНИКЕ ТРЕЩИН // Современные наукоемкие технологии. – 2014. – № 2. – С. 56-60;URL: https://top-technologies.ru/ru/article/view?id=33651 (дата обращения: 21.11.2024).