Задачами функционального анализа являются постановка целей и задач для теоретических исследований, которая решается с использованием методов функционального анализа. Наибольшее распространение получил метод системного анализа функций FAST – (Functional Analisis Sistem Techigue) который был предложен Г. Байтуэем. Существо метода FAST сводится к построению и анализу функций (функциональной модели).
На функциональной модели исследуемая задача представляется в виде логической цепочки функций, которые разделяются на четыре иерархических уровня: высший, главный, основной и низший. Рамки исследуемой задачи (проблемы) ограничиваются двумя вертикальными (в нашем случае горизонтальными) пунктирными (штрих пунктирными) линиями, между которыми располагаются анализируемые функции. Нижняя граничная линия отделяет главную функцию, которая располагается над линией, от функции низшего уровня от основных функций [1].
Функция высшего уровня характеризует цель, на достижение которой направлено действие или для достижения которой предназначена результат действия главной функции анализируемой подсистемы (объекта), являющегося составной частью системы.
Функция низшего уровня является как бы первопричиной существования или появления анализируемой системы (объекта).
Одной из важнейших особенностей построения диаграммы FAST является выявление функций критического пути. Любая функция, формулировка которой умещается в логическую схему, определяемую вопросами: «как?», «почему?», зачем?», и описание которой (ответ на вопрос) не противоречит здравому смыслу, является функцией критического пути. На функции критической дуги располагаются те функции, которые обязательно должны быть осуществлены для реализации главной функции, т.е. основные функции. Различают функции главного критического пути, т.е. основные внутриобъектыне функции, описывающие главную функцию системы «объекта» , и малого критического пути, т.е. вспомогательные функции этой же системы (объект), описывающую какую либо независимую вспомогательную функцию, способствующую реализации одной из основных и проявляемую одновременно с ней. Указанные, независимые вспомогательные функции в другой подсистеме могли бы стать главным и входить в совершенно другую систему [2].
Выбор концепции в процессе анализа принципиально нового (с новым набором основных функций) зависит от характера исследуемой задачи уровня предложенного решения.
С использованием методики FAST разработана общая функциональная модель системы микроГЭС.
Функции низшего уровня расположены на самом верху, над верхней линией. Они явились концепцией для образования системы и от них исходят связи новой структуры. Функции низшего уровня формулируются, как максимально использовать гидравлическую энергию, который характеризуется напором и расходом воды.
Функций высшего уровня два: энергоснабжение малоэнергоемких потребителей и автономность источников энергии. Основные функции расположены на линиях главного критического пути.
В подсистеме гидротурбины первой функции является использовать энергию воды (ЭВ). Второй, энергию воды преобразовать в механическую энергию и передать генератору. Процесс осуществляется в три отличающихся по физической природе этапа. На первом, этапе энергия представляет собой кинетической или потенциальной поток т.е. энергии водотока. Во втором, водная энергия утилизируется и преобразовывается в механическую энергию вращения гидротурбин. В третьем механическая энергия вращения гидротурбин передается генератору.
Преобразование поглощенной кинетической или потенциальной энергии воды в электрическую энергию осуществляется микроГЭСом в три этапа:
Первый –подвод воды напорным трубопроводом, где энергия водотока подготавливается для гидротурбин для создания соответствующего напора;
Второй – созданием циркуляции потока перед входом на рабочее колесо, где выполняется следующие функции закручивание потока, регулирование расхода и остановка турбины;
Третий – преобразование энергии потока в механическую энергию турбины или рабочего колеса. При вращении турбин получаем полезный крутящий момент, который через вал передается генератору.
Эффективность работы микро-гидростанций зависит от оптимальной и согласованной работы турбины, электрогенератора и системы управления.
Устойчивая работа системы турбина – генератор возможна при положительном значении суммарного коэффициента устойчивости, которые нужно обеспечить при поддержании постоянства напряжения у потребителя. Момент генератора зависит мощности и угловой скорости генератора.
Анализ электрической части известных конструкций микрогидроэлектростанций показал, что в микроГЭС широкое применение нашли синхронные и асинхронные генераторы. Разработка автоматизированных микро-гидроэлектростанций (микро-ГЭС) требует проведения глубоких исследований. Изменение энергии водного потока и колебания нагрузки усложняют задачу обеспечения постоянства напряжения и частоты тока. Сложность и дороговизна управления водным потоком поступающего на гидродвигатель, вызвала тенденцию к упрощению гидротехнической части станции, что сопровождается повышением требований к электрической части.
Переходные процессы, вызванные нестабильностью энергии поступающей на гидродвигатель, протекают динамичнее, что также повышает требования к электрической части установок.
С использованием функциональных моделей разработаны информационные модели для теоретического анализа подсистем. При этом элементы информационной модели наделены функциями определенными.
Общие формализованные модели системы микроГЭС
Формализованная модель устанавливает обобщенные параметрические взаимосвязи между элементами по схеме «вход – процесс– выход». В качестве входных принимаются внешние управляемые воздействия, а выходными, ожидаемые показатели элементов [3].
С учетом выше изложенного систему микроГЭС можно представить виде структурной схемы «водный поток–напорный трубопровод–гидротурбина–генератора–аккумулятор»
Такой подход позволяет соблюсти принцип системности, поскольку объект представляется в виде системы, преобразующей входные переменные в выходные, а анализ, синтез и оптимизация параметров осуществляется на основе исследования закономерностей процессов между входными и выходными параметрами.
Как известно, в общем случае модель сложного процесса представляется в виде многомерной системы, на входе подсистем которых действуют векторные функции:
– условий функционирования
F(τ)=[F1(τ)·F2(τ)∙F3(τ)∙F4(τ)]; (1)
– условий управления
U(τ)=[U1(τ);U2(τ);U3(τ);U4(τ)] . (2)
А выходные переменные образуют векторные функции
Y(τ)=[y1(τ);y2(τ);y3(τ);y4(τ)]. (3)
Математическая модель системы является тем абстрактным формально описанным объектом, изучение которого возможно математическими методами, в том числе с помощью математической модели. Сложность и многообразие процессов функционирования не позволяет строить для них абсолютно адекватные математические модели. Математическая модель, описывающая формализованный процесс функционирования системы, в состоянии охватить только основные, характерные его закономерности, оставляя в стороне несущественные второстепенные факторы. Формализация любого реального процесса предшествует изучение структуры составляющих его элементов и явлений, целью которого, в конечном итоге, является синтез оптимальной структуры.
Такое представление модели функционирования системы дает возможность получить их математические описание. Математическое моделирование заключается в определении агрегата или установки (А) т.е. в установлении вида и характера преобразования входных векторных функций (F) и (U) в выходные (Y).
Y=A(F,U). (4)
Для любой пары векторных функций Fn(τ) Yn(τ) в интервале наблюдения τ0< τ<τn существует:
Yn(τ)=An [Fn(τ)]. (5)
В общем случае компоненты Fn(τ) и Yn(τ) являются случайными процессами и задаются множеством реализаций:
Fn(τ)={fn1(τ); fn2(τ)… fni(τ)}; (6)
Yn(τ)={yn1(τ); yn2(τ)… yni(τ)}. (7)
Поэтому при описании сложных систем для каждого выходного компонента имеются Ani операторов. Исследуемые подсистемы можно представить виде следующей функционально-структурной модели (рис. 1).
Первая направляющая подсистема подготавливает энергию водотока для гидротурбин для создания соответствующего напора и имеет входные переменные, и имеет собственные пространственно-временные характеристики.
Y1(τ) Y2(τ) Y3(τ) Y4(τ)
Рис. 1. Функционально-структурная модель: 1 – напорный трубопровод; 2 – гидротурбина; 3 – генератор; 4 – аккумулятор-потребитель
Для водной энергии таковой является мощность водного потока, которая переменна во времени и в пространстве
Y1(τ)=Wвэ(t). (8)
Энергия потока состоит из энергии положения z1-z2, энергии давления (образующих вместе потенциальную энергию), а также кинетической энергии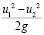 
, которая имеет собственную закономерность
Y1(τ)=Wэп(t; z; u). (9)
Турбины, хотя бы частично использующие потенциальную энергию, называются реактивными, имеет те же свойства – переменность во времени и в пространстве. В таких турбинах
,
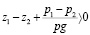и, следовательно, процесс преобразования энергии на рабочем колесе происходит с избытком давления.
Y1(τ)=Wпэ(τ; z; u). (10)
Для активных турбин выполняется, условие z1=z2, p1=p2, т. е. вода поступает на рабочее колесо без избыточного давления. Для достижения высокого КПД в них почти весь напор преобразуется в скорость.
Следовательно, для активных турбин энергия потока зависит от массы или скорости потока.
Y1(τ)=Wэп(mв; u). (11)
Основными уравнениями исследуемой системы являются:
Y1(τ)= F2(τ)= Wвэ(τ)+ Wэп(τ; z; u)+ Wпэ(t; z; u;p)+ Wэп(mв; u); (12)
Y2(τ)=F3(τ)=[ Wвэ(t)+ Wпэ(t; z; u; p)] ηмех турб. ; (13)
Y3(τ)=F4(τ)= F3(τ) + Pген(Uген; nген); (14)
Y4(τ)=W(τ)=Pтурб(τ)ηт+ Pакт(t) ηт – Pпотр(t); (15)
В зависимости от режима подсистемы «микроГЭС–генератор–аккумулятор–потребитель» выполняются следующие условия:
Y4(τ)>0 режим избытка вырабатываемой мощности;
Y4(τ)= 0 режим равенства мощностей;
Y4(τ) < 0 режим недостатка мощности.
Таким образом, проведенным анализом обосновано сложное структурно-функциональное устройство ССТС. Установлены обобщенные, формализованные математические соотношения показывают и подтверждают, что рассматривая система не просто сумма простых систем, а взаимосвязанная взаимообусловленная совокупность явлений и процессов.
Выводы. Нами выполнены функционально-структурный анализ системы микроГЭС, с использованием функциональной моделей, разработаны информационные модели для теоретического анализа подсистем, при этом элементы информационной модели наделены функциями определенными FAST диаграммами [1].
Библиографическая ссылка
Умбетов Е.С., Бакенов К.А. ФУНКЦИОНАЛЬНЫЙ И СТРУКТУРНЫЙ АНАЛИЗ СИСТЕМЫ МИКРОГЭС // Современные наукоемкие технологии. – 2014. – № 1. – С. 52-55;URL: https://top-technologies.ru/ru/article/view?id=33630 (дата обращения: 19.04.2024).