Проанализируем возможное влияние типа механизма локального проявления структурных элементов 4D Р-ячейки на геометрико-топологические свойства и структурные состояния транзитивной области 3D ячеистого пространства. Для этого рассмотрим некоторые топологические характеристики структурированного пространства, представляющего собой клеточный комплекс. В соответствии с теоремой Эйлера целочисленная характеристика конечного клеточного комплекса К
,
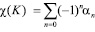где αn – число n-мерных клеток комплекса (или n-мерных структурных элементов полиэдра), является гомологическим, гомотопическим и топологическим инвариантом и не зависит от способа разбиения пространства на клетки (ячейки) [1, 2].
С другой стороны эйлерова характеристика может быть представлена следующим образом:
,
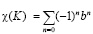где bn – n-мерное Бетти число комплекса K, а эйлерова характеристика c(K) является топологическим инвариантом n-мерного полиэдра и равна числу попарно негомологичных циклов в нем.
Для компактного n-мерного полиэдра c(K) = 2. В связи с этим будем рассматривать функцию
(c(K) + x)n = (2 + x)n
и соответствующее разложение этой функции в ряд Маклорена
2n + n 2n-1 x +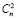 
2n-2 x2 + 
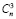2n-3 x3+…+ + 
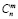2n-m xm +…+ 
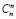20 xn,
с областью сходимости |x| < 2. Здесь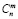 
– биномиальные коэффициенты, численно равные количеству сочетаний из n по m.
В соответствии с формулой Эйлера-Пуанкаре имеем корреляцию с эйлеровой характеристикой c(K), если в алгебраической сумме коэффициентов ряда Маклорена
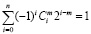
учитывать все структурные элементы выпуклого n-мерного полиэдра с размерностями m < n, а также и сам полиэдр.
Если n-мерный полиэдр определен в единичной ячейке n-мерного пространства, т.е. в клетке, построенной на интервалах [0,1] n 1D подпространств, то x = 1. Тогда общее количество всех структурных элементов n-мерного полиэдра с размерностями m < n с учетом самого полиэдра равно
Nstr. el. = [(2 + x)n –1]= (3n – 1).
Общее количество определенных структурных элементов с размерностью n’ < n, составляющих n-мерную фигуру, можно определить по следующей формуле:
.
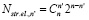Общее количество определенных структурных элементов (т.е. с определенными размерностями n’ < n) n-мерных фигур, плотно упакованных в nD пространстве, которые имеют общую вершину, может быть рассчитано с учетом замены (n–n’) → n’ по аналогичной формуле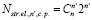 
.
В соответствии с теоремой Штейница существует выпуклый многогранник с любой наперед заданной сеткой, составленной его ребрами. В частности, для выпуклых шестигранников существует 7 типов сеток, одной из которых является кубическая. Куб – правильный многогранник, один из пяти тел Платона, является изоэдром с квадратными гранями и изогоном (многогранником с топологически идентичными вершинами). Куб – параллелоэдр, позволяющий получить нормальное разбиение [1]. При плотной упаковке в 3D пространстве из его ребер образуется кубическая сетка, а из геометрических центров – кубическая решетка. По аналогии с нормальным разбиением в 3D пространстве на кубические ячейки существуют нормальные разбиения гиперпространств на соответствующие гиперкубические ячейки [2]. Топологические характеристики некоторых n–мерных фигур приведены в табл. 1.
Для определения влияния механизма локального проявления 4D Р-ячейки на геометрико-топологические свойства и структурные состояния транзитивной области 3D пространства будем рассматривать механизм замещения структурного элемента пространственной Р-ячейки и механизм внедрения в область существования этого элемента. Оба типа механизма проявления гиперпространства в ячеистом 3D пространстве сопровождаются изменением геометрико-топологических характеристик его Р-ячеек, в частности, изменением объемной концентрации ее определенных структурных элементов (вершин, ребер). Эти изменения охватывают определенную локальную область пространства – транзитивную область, включающую также и замещающий (или внедренный) структурный элемент 4D Р-ячейки.
Таблица 1
Топологические характеристики некоторых n–мерных фигур
|
Фигура |
Общее количество определенных структурных элементов плотно упакованных в nD пространстве n-мерных фигур, имеющих общую вершину |
Мерность пространства плотно упакованных фигур, n’ |
||||
|
Общее количество определенных структурных элементов фигуры, Nstr. el. |
||||||
|
Структурные элементы и их размерности n’ |
||||||
|
вершина (0) |
ребро (1) |
грань (2) |
3D куб |
4D куб |
||
|
точка |
1 |
2 |
4 |
8 |
16 |
0 |
|
отрезок |
2 |
1 |
4 |
12 |
32 |
1 |
|
квадрат |
4 |
4 |
1 |
6 |
24 |
2 |
|
3D куб |
8 |
12 |
6 |
1 |
8 |
3 |
|
4D куб |
16 |
32 |
24 |
8 |
1 |
4 |
В предположении о сохранении объема пространственной Р-ячейки в процессах проявления в ней структурных элементов 4D Р-ячейки (т.е. ∆V = 0) будем рассматривать следующие характеристики транзитивной области.
1. Усредненное изменение объемной концентрации вершин DCv = (∆Nv/Vяч.).
В 3D Р-ячейке (примитивной кубической ячейке) Nv =1.
2. Относительное изменение суммарной длины ребер всех структурных компонентов транзитивной области DLr = (DLp/Lp).
В 3D Р-ячейке Lp = 3a , где a – метрический параметр кубической ячейки.
Влияние механизма проявления структурных элементов Р-ячейки 4D пространства на объемную концентрацию вершин и суммарную длину ребер всех компонентов транзитивной области представлено в табл. 2. Очевидно, что при реализации механизма замещения объемная концентрация вершин закономерно увеличивается с уменьшением мерности замещаемого структурного элемента и увеличением мерности элемента-заместителя. При реализации механизма внедрения величина изменения характеристики Cv транзитивной области более существенна (табл. 2). Для характеристики DLr транзитивной области качественный характер изменений для одного и другого механизма аналогичен, однако он усложняется при совпадении мерности структурных элементов 3D и 4D Р-ячеек (табл. 2).
Приведем примеры некоторых классов веществ [3-25], структурные особенности которых в локальной области могут быть интерпретированы в рамках возможного влияния одного из механизмов проявления структурных элементов гипотетической 4D Р-ячейки.
Таблица 2
Влияние механизма проявления структурных элементов Р-ячейки 4D пространства на удельные геометрические характеристики транзитивной области
|
Структурные элементы |
Удельные геометрические характеристики транзитивной области |
||||
|
Механизм замещения |
Механизм внедрения |
||||
|
3D ячейка |
4D ячейка |
Cv |
Lr |
Cv |
Lr |
|
вершина |
вершина |
1,000 |
3,00 |
- |
- |
|
ребро |
1,123 |
4,20 |
1,250 |
4,83 |
|
|
грань |
1,375 |
4,34 |
1,500 |
4,81 |
|
|
ячейка |
1,875 |
6,43 |
2,000 |
7,10 |
|
|
ребро |
вершина |
0,917 |
4,71 |
1,083 |
4,12 |
|
ребро |
1,000 |
3,00 |
- |
- |
|
|
грань |
1,167 |
4,49 |
1,333 |
4,74 |
|
|
ячейка |
1,500 |
6,72 |
1,667 |
7,96 |
|
|
грань |
вершина |
0,833 |
4,97 |
1,056 |
5,88 |
|
ребро |
0,888 |
4,42 |
1,111 |
5,05 |
|
|
грань |
1,000 |
3,00 |
- |
- |
|
|
ячейка |
1,222 |
7,89 |
1,444 |
8,66 |
|
|
ячейка |
вершина |
0,741 |
6,83 |
1,037 |
9,93 |
|
ребро |
0,778 |
5,22 |
1,074 |
7,24 |
|
|
грань |
0,852 |
4,54 |
1,148 |
5,43 |
|
|
ячейка |
1,000 |
3,00 |
- |
- |
|
В модулярных структурах на основе структурного типа шпинели с использованием модуля состава AB2X4 [3-12] также могут быть получены шпинелоиды-гомологи, принадлежащие, в частности, рядам окисления An+2(B2X4)3n, A2n+1(B2X4)2n, A3n+3(B2X4)3n, A3n+1(B2X4)4n и ряду восстановления вида A2n-1(B2X4)4n [8, 12]. Изменение вершинной топологии тетраэдров от 4(2) к 2(2)-2(3) в плоскостях сдвига приводит к изменению в предполагаемой транзитивной области объемной концентрации вершин DCv = 0,187, а изменение вершинной топологии октаэдров от 6(2) к 3(2)-3(3) – к изменению DCv = 0,100.
В системах сложных оксидов переходных металлов с октаэдрическими структурами известны гомологические ряды окисления: MenOn-1 (Me – Cr, V), MenO2n-1 (Me – Ti, Mn, V, Nb), MenO3n-1 и MenO3n-2 (Me – W, Mo), VnO5n-2, MenO8n-3 (Me – V, Nb), и гомологические ряды восстановления MenOn+1 и MenO2n+1 (Me – V, Nb) [8, 13-15]. Эти гомологические ряды характеризуют фазы кристаллографического сдвига и, как показано в [16, 17], могут быть представлены следующим образом: ряды окисления – Me3F(n) – F(n-2)OF(n) и Me2F(n) – F(n-2)OF(n), ряды восстановления – MeF(n) + F(n+1)OF(n) и MeF(n) + F(n-1)OF(n), где F(n) – числа Фибоначчи. Определена область вероятного существования оксидов переходных металлов с октаэдрическими структурами состава MeaOb : (1+t) ≤ (b/a)≤ ≤ (3–t), где t ≅ 0,62 – численное выражение золотого сечения [2] Установлено, что изменение вершинной топологии октаэдров от 6(2) к 3(2)–3(3) в плоскостях сдвига приводит к изменению в предполагаемой транзитивной области объемной концентрации вершин на величину DCv = 0,125.
В литийсодержащих фазах внедрения на основе олова и свинца существуют две гомологические серии структур Li3n-2Men и Li5n-2Men (n = 2 – 6, ∝ Me – Sn, Pb), которые в [8, 18, 19] представлены как следствие одномерного и двумерного кристаллографического сдвига в структурах исходных металлов. При изменении порядкового номера n от 2 до 6 величина параметра изменения атомной плотности DCv для гомологов двух рядов закономерно возрастает от 0,333 до 0,455 (в сравнении с гомологом при n = 1).
Упорядоченные твердые растворы внедрения лития в гексагональный графит образуют серию структур состава LixC (где x = 1/6, 1/8, 1/10, 1/12, 1/14, 1/18) [8, 20, 21]. Упорядоченные твердые растворы внедрения лития в диоксид металла образуют в свою очередь серию структур состава LixMeO2 (где x = 1/3, 1/4, 1/6, 1/9, 1/12, 1/16) [8]. Параметр изменения атомной плотности DCv для представителей этих двух серий структур принимает значения в интервале 0,056 – 0,187 и 0,021 – 0,111, соответственно.
Для карбидов некоторых переходных металлов возможно образование упорядоченных фаз состава MeaCb, где (b/a) = 1–x0, а параметр x0, характеризующий отклонение от стехиометрии, может принимать определенные значения, например, 1/4 (V4C3), 1/6 (V6C5) и 1/8 (V8C7) [21-25]. Соответствующие значения параметра изменения атомной плотности DCv = – 0,250, – 0,167 и – 0,125.
Таким образом, перечисленные выше примеры локального изменения атомной плотности формально могут быть интерпретированы как различные варианты возможного проявления некоторых структурных элементов гипотетической гиперячейки в структурированном 3D ячеистом кристаллическом пространстве.
Результаты работы получены при поддержке Минобрнауки РФ в рамках государственного задания на проведение НИОКР, шифр заявки N6.8604.2013.
Библиографическая ссылка
Иванов В.В., Таланов В.М. ВЛИЯНИЕ ТИПА МЕХАНИЗМА ЛОКАЛЬНОГО ПРОЯВЛЕНИЯ СТРУКТУРНЫХ ЭЛЕМЕНТОВ 4D Р-ЯЧЕЙКИ НА ГЕОМЕТРИКО-ТОПОЛОГИЧЕСКИЕ СВОЙСТВА И СТРУКТУРНЫЕ СОСТОЯНИЯ ТРАНЗИТИВНОЙ ОБЛАСТИ 3D ЯЧЕИСТОГО ПРОСТРАНСТВА // Современные наукоемкие технологии. – 2014. – № 1. – С. 34-37;URL: https://top-technologies.ru/ru/article/view?id=33625 (дата обращения: 21.11.2024).