Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бескровный И.М. 1

---

1 OAO «Ангстрем-М»

Целью работы является продолжение исследований, проведенных в [1, 2]. В этих работах исследовалась проблема разделения многомерных структур класса ln на слагаемые того же класса. В итоге, были получены расчётные соотношения для n=2. И начаты исследования для n=3. В настоящей работе исследования продолжены для показателя n=3 и получены результаты для показателей степени n= 4,5,6. Доказано, что при разделении многомерных структур класса ln на слагаемые, с тем же показателем степени минимальное количество слагаемых определяется показателем степени, то есть, соотношением . Сформулирована теорема, утверждающая, что сумма из n многомерных структур класса ln может быть отображена единственной структурой, имеющей тот же показатель степени. То есть, для соотношения вида существуют целочисленные решения. В качестве примера приведены числовые значения решений для значений n=2,3,4,5.

Статья в формате PDF

967 KB

многомерные геометрические структуры

разделение куба

системный анализ

математическая модель

графическая модель

теорема Ферма

1. Бескровный И.М.. Системный анализ пифагоровых троек // Современные наукоёмкие технологии, № 11, 2013.

2. Бескровный И.М. Алгебра геометрических фигур и геометрия алгебраических формул // Современные наукоёмкие технологии, № 11, 2013.

3. Сингх С. Великая теорема Ферма. – URL: http://royallib.ru/book/singh_saymon/velikaya_teorema_ferma.html.

4. Ферма П. Исследования по теории чисел и диофантову анализу. – М.: Наука, 1992.

Известно, что Ферма, исследуя свойства пифагоровых троек вида задался вопросом, а не существует ли решение для подобных по структуре уравнений при других показателя показателях степени [3, 4]. То есть, может ли сумма двух слагаемых с показателями степени n, быть равна одному числу, возведенному в ту же степень. Иными словами – существует ли решение для уравнений вида

. (1)

В итоге он сформулировал свою Великую Теорему, утверждающую решения для уравнения (1) при n>2 решения не существует.

Однако остался открытым вопрос, а не существует ли для n>2 решения для уравнений, имеющих в левой части уравнения количество слагаемых больше двух? Ответ на этот вопрос был получен в работе [2], где было показано, что такие решения существуют для куба, который успешно делится на три части. Успешное решение задачи при n=3 дало основания выдвинуть гипотезу, что проблема разделения любого числа вида ln на несколько слагаемых при произвольном значении n имеет целочисленное решение. При этом количество слагаемых не может быть меньшим, чем значение показателя степени n. То есть, имеет место закономерность вида

. (2)

В работе [2] на основе системного анализа и экспериментальной проверки было показано, что для кубов это минимальное число, обозначенное Qmin, равно трём. То есть, при делении куба на целочисленные блоки выполняется равенство

(3)

и образуются четвёрки чисел где первые три числа – длины рёбер слагаемых кубов и четвёртое число – длина ребра их суммы. В работе [2] такие четвёрки названы квадригами и установлено, что соблюдение равенства (3) достаточно регулярно наблюдается. Так в диапазоне первых трёх сотен числового ряда было найдено 10 таких квадриг.

В следующем разделе приводится системное обоснование, почему квадрат можно разделить на две части, а для куба минимальное количество частей, на которое его можно разделить, равно трём.

Итак, если записать соотношения (1) и (3) таким образом:

(4)

то возникает естественное желание продолжить складывающуюся последовательность и записать её в следующем виде:

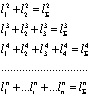(5)

Запись соотношения (5) отображает в иной форме математическую формулировку о том, на какое минимальное количество Qmin может быть разделена геометрическая фигура, то есть, иную формулировку соотношения (2).

Успешное подтверждение существования квадриг доказало справедливость первых двух уравнений в последовательности (5) дало основания для дальнейшего анализа входящих в эту последовательность уравнений, имея в виду перевод выдвинутой в [2] гипотезы в ранг теоремы. Таким образом, цель настоящей работы заключается в том, чтобы дать дополнительные обоснования справедливости уравнений в последовательности (5) для показателей степени n=3,4,5,6.

Постановка задачи, основные определения

Алгебраическое решение для уравнений, составляющих последовательности (5), для первых двух уравнений: а для n=2,3 как будет показано в данном разделе, получить несложно. Но, для n>4 уравнения становятся настолько громоздкими, что для поиска решений предпочтительным становится другой подход, предложенный в [2]. Он базируется на модельном представлении величин вида ln в виде многомерных геометрических структур. Под многомерной геометрической структурой будем понимать некий каркас или замкнутый граф, образованный ребрами одинаковой длины l и нулевой толщины. Все концы рёбер соединены друг с другом. Свободных концов нет. Все ребра ориентированы только параллельно осям координат и ортогонально друг другу.

При таких определениях выражение ln становится математической моделью геометрической структуры. И в этой модели содержится следующая информация:

Величина l – длина ребра, выраженная натуральным числом; n – пространственная размерность структуры, то есть, число измерений в пространстве, в котором размещена структура.

Применительно к задаче разделения на блоки, такую многомерную структуру можно рассматривать как контейнер, содержащий ln элементарных ячеек вида 1n. При n=2 имеем квадрат, площадь которого составляет l2 элементарных квадратиков 12 нулевой толщины. При n=3 получаем куб, объём которого измеряется количеством l3 элементарных кубиков единичного объёма 13 и т.д. Тогда задачу разделения многомерной структуры на несколько подобных ей структур (на блоки) той же размерности можно рассматривать как задачу целочисленного программирования, сформулированную следующим образом.

Содержание многомерного контейнера емкостью ln элементарных ячеек требуется разместить в несколько контейнеров меньшей емкости таким образом, чтобы каждый из контейнеров был заполнен полностью, и количество использованных контейнеров было минимальным. Ассортимент контейнеров строго регламентируется значением показателя степени и состоит из контейнеров, имеющих емкость

. (6)

При этом количество каждого из контейнеров определённой ёмкости не лимитировано. То есть, при наличии потребности может быть использовано несколько одинаковых контейнеров емкостью
.

Введенные определения позволяют увидеть проблему разделения многомерных геометрических структур в более наглядном виде. Например, при вычитании из площади квадрата l2 площади меньшего квадрата в остатке остаются две полосы нулевой толщины, состоящие из элементарных квадратов в количестве l и l–1 (см. рис. 1). Чтобы из этого остатка мог быть сформирован второй квадрат емкостью надо определить такое значение величины x, при котором становится справедливым равенство

, (7)

из которого следует уравнение

. (8)

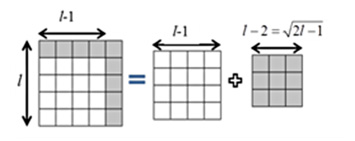
Рис. 1. Графическая модель разложения квадрата

Решение уравнения (8) существует для любого значения l, но целочисленным оно является только при условии, что величина является натуральным числом.

Бесконечная последовательность чисел, удовлетворяющих требованию целочисленности решения для уравнения (8) имеет вид

5, 13, 25, 41, 61, 85,…… (9)

Легко заметить, что в этой последовательности каждое из чисел отстоит от предыдущего на величину, кратную 4. Пронумеруем их последовательно, начиная с минимального. Тогда приведенный выше ряд чисел, можно представить соотношением

, (10)

из которого следует:

, (11)

Как видно из соотношений (9), (10) интервалы между соседними значениями li нарастают весьма быстро. Так, например, после допустимого значения , следующее допустимое значение , а после , следующее допустимое значение , то есть, допустимое значение отстоит от предыдущего более чем на пятьдесят миллионов! Очевидно, что именно по этой причине и появилась в книге С. Сингха такая фраза – «По мере того, как числа возрастают, пифагоровы тройки встречаются все реже, и находить их становится все труднее и труднее…» [3]. Но, на самом деле триады надо не «находить», а вычислять. Пользуясь, например, формулами, полученными выше, а также дополнительными формулами, полученными в [1].

При вычитании из куба l3 куба с длиной ребра, меньшей на единицу, картина будет иной (рис. 2). Теперь в остатке остаются три пласта единичной толщины и с площадями l2 – слева, l(l–1) – сверху и (l–1)2 – сзади. Общее количество элементарных кубиков в остатке составляет

. (12)

Значит, обеспечения делимости куба на два целочисленных блока требуется выполнение равенства

, (13)

что соответствует уравнению

. (14)

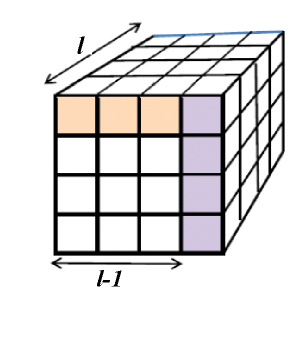
Рис. 2. Разделение куба

Экспериментальная проверка показала, что в диапазоне значений уравнение (14) целочисленных решений не имеет. Например, при l=6, уравнение (14) имеет три корня:

Отсутствие целочисленных решений означает, что сформировать из правой части уравнения (13) один куб невозможно. Связано это, по всей очевидности, с тем, что величина l входит в этот остаток с двумя показателями степени: n=1, и l=2. Тогда как для квадрата в правой части соотношения (7) величина l входит только в первой степени.

Поскольку приведенные аргументы и экспериментальное подтверждение того, что для куба справедливо соотношение

, (15)

то алгебраическое решение для определения всех элементов квадриги в общем случае можно найти из следующего уравнения

, (16)

то есть, получаем кубическое уравнение с тремя переменными и это, конечно не подарок.

Задачу можно упростить, исходя из следующих соображений. С целью минимизации общего количества кубов, вычитаемых из исходного, величину первого вычитаемого куба принимаем не меньше, чем . Далее, заменим одну из двух оставшихся переменных константой k, то есть, представим соотношение (16) в следующем виде

, (17)

откуда следует уравнение

(19)

В табл. 1 приведены решения уравнения (17) для значений . Эти решения соответствуют первым двум и последним двум квадригам из 10 квадриг, найденных в [2] в диапазоне чисел
.

Таблица 1

Параметры квадриг

Конечно, отыскивать неизвестные квадриги непосредственно с помощью уравнения (19) задача неподъёмная. Главным образом потому, что целочисленные корни это уравнение имеет только для «решабельных» значений l, которые необходимо знать a-priori. Поэтому все 10 квадриг, представленных в табл. 2, отыскивались по методу, названному нами методом направленного спуска. Из очередного значения вычиталось значение . Затем из полученной разности вычиталось значение . Это значение подбиралось из таблицы кубов так, чтобы оно было наиболее близким к предыдущему вычитаемому. Таким же образом производилось и третье вычитание. Если остаток после третьего вычитания является кубом, значит, найдена очередная квадрига.

Таблица 2

Значения квадриг

В значениях квадриг, приведенных в табл. 2 не удается выявить какую либо закономерность в появлении таких значений l, для которых квадриги существуют, как это имело место при формировании триад. Это ещё раз подчеркивает системную зависимость значения величины Qmin только значения от показателя степени n и от геометрических свойств соответствующей данному значению структуры, а вовсе не от специфических свойств чисел, из которых образуются триады, квадриги и т.д.

Примечательной в табл. 5 является первая квадрига, числовые значения которой соответствуют кубу с ребром 6, разделённому три куба с рёбрами 5, 4, 3, что соответствует сторонам квадратов в первой триаде. В последующих квадригах подобные совпадения не встречаются.

Далее, по методу направленного спуска для значений n=4,5,6 был проведен поиск случаев разделения на число блоков, определяемое соотношением

. (20)

В результате, при n=4 в диапазоне чисел 1–2500 было найдено 4 случая деления на 5 блоков, 10 случаев деления на 6 блоков и 25 случаев деления на 7 блоков. При n=5 минимальное число слагаемых, на которое можно разделить пятую степень, оказалось равным 6. При n=6 в указанном диапазоне чисел шестимерники разделялись на количество блоков, большее, чем 6.

Более подробных исследований, с использованием других стратегий поиска и т. д. не проводилось. Полученные результаты полностью удовлетворяют поставленным целям и дальнейшие более подробные исследования выходят за рамки данной работы.

Заключение

Проведенные в настоящей работе исследования полностью подтвердили справедливость выдвинутой в [2] гипотезы о том, что при разделении многомерных структур класса ln на блоки той же степени минимальное количество таких блоков звисит отпоказателя степени, то есть, определяется соотношением . Полученные результаты дают основание перевести эту гипотезу в ранг теоремы, формулируемой следующим образом:

Теорема: Многомерная структура класса ln может быть отображена суммой структурой, имеющих тот же показатель степени при условии, что количество слагаемых в этой сумме не меньше значения показателя степени n. То есть, при соблюдении условия, что .

Доказательство. Справедливость уравнения при доказана теоремой Пифагора, при n=3,4,5,6 подтверждена экспериментально. Численный пример приводится ниже:

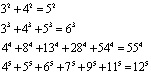(21)

Результаты, полученные в данной работе, можно было бы рассматривать как ещё один вариант доказательства теоремы Ферма. Однако, если доказано, что степени 3, 4, 5, 6 делятся на блоки тех же степеней, в количестве, не меньшем, чем показатель степени, то доказательство того, что они не делятся на два таких блока становится избыточным.

Библиографическая ссылка