Известные кристаллохимические явления, такие как изоморфизм, морфотропия, полиморфизм, политипия, структурная гомология и др., характеризуют те или иные родственные отношения между различными структурными типами веществ [1-5]. Некоторым из этих явлений, например, изоморфизму, морфотропии и полиморфизму, соответствуют реальные физико-химические процессы (в данном случае процессы внедрения-вычитания, фазовые превращения). Однако большинство кристаллохимических явлений, в т.ч. политипия, гомеотипия и структурная гомология, представляют собой результат установления определенной родственной связи между структурами на основе их сравнительного анализа и не соответствуют каким-то определенным физико-химическим процессам в химических системах.
Факты проявления аномалий кристаллохимической и геометрической топологии структур или их определенных структурных элементов не всегда удается объяснить каким-либо определенным физико-химическим процессом, связывающим данную аномальную структуру с ее вероятным структурным «родственником». В качестве примеров можно привести случаи проявления аномальной гиперкоординации атомов [6, 7], аномально высокой или низкой атомной плотности в фрагментах 3D структур с мерностью меньше трех [8-19] и в локальных областях модулярных структур [4, 20-27], возможных квазифрактальных фрагментов в 3D структурах, аномальной апериодичности и квазикристаллических состояний 3D структур [28-37].
Допущение возможности процесса локального проявления вполне определенных гиперструктурных особенностей в кристаллических 3D структурах не подразумевает под собой какого-либо реального физического или физико-химического процесса. Однако именно предположение о проявлении дополнительного гиперпространственного измерения позволяет по-новому интерпретировать большинство кристаллохимических явлений и некоторые кристаллохимические и структурные аномалии в строении кристаллов.
Проблема определения вероятной взаимосвязи геометрических свойств определенных 3D структур с аналогичными геометрическими свойствами 4D структур, а также возможного количественного и качественного влияния вида гиперпространственных структурных дополнений 3D структур на некоторые физико-химические свойства их представителей, может быть основана на решении следующих двух групп задач.
Прямые задачи:
– определение вероятных гиперячеек 4D структур, 3D сечения которых и развертки 3D «поверхности» соответствуют заданной 3D структуре,
– идентификация вероятных структурных «продолжений» заданной ячейки 3D структуры в дополнительном измерении гиперпространства.
Обратные задачи:
– определение вероятных ячеек 3D структур, соответствующих заданному симметричному сечению гиперячеек 4D структуры и заданной симметричной развертке 3D ее «поверхности»,
– определение остальных соответствующих симметричных сечений меньшей мерности и идентификация ячеек 3D структуры, «продолжение» которых в дополнительном пространственном измерении приводит к формированию гиперячеек 4D структуры.
Актуальность решения этих задач вызвана необходимостью
1) определения топологических характеристик nD и (n-1)D-структур с целью выявления закономерностей их изменения (морфизмов) при переходах nD структура « (n-1)D структура,
2) установления новой генетической связи как между 3D структурами, имеющими одинаковые «продолжения» в гиперпространственном измерении, так и между 4D структурами, производными от одной и той же 3D структуры,
3) определения роли возможного структурного синергизма в проявлении качественно одинаковых свойств 3D структурами с одинаковыми «продолжениями» в гиперпространственном измерении, и в проявлении качественно разных свойств 4D структурами, производными от одной и той же 3D структуры,
4) формирования синергической модели, описывающей изменение некоторых свойств 3D структур при учете гиперпространственного измерения и интерпретации роли возможного структурного синергизма,
5) разработки прогнозной модели условий формирования 3D структур неорганических веществ с необходимым уровнем проявления физико-химических свойств, а также кристаллических веществ с аномальными свойствами, не характерными для представителей анализируемого структурного типа.
Рассмотрим следующие способы определения образа 4D структуры в 4D пространстве и определения его основных топологических характеристик (количества и конфигураций структурных элементов с меньшими размерностями и их локальной топологии, симметричной формы представления структуры и ее возможных топологических производных):
1) восстановление образа гиперячейки 4D структуры по достаточной совокупности ее проективных изображений в пространстве меньшей мерности, или по симметричной развертке ее 3D «поверхности» в 3D пространстве,
2) получение интегрированного образа гиперячейки 4D структуры по конечным сериям ее симметричных сечений, или сечений ее развертки.
Для реализации этих способов будем придерживаться следующих предположений.
Предположение 1. Если существует изображение (образ) гиперячейки 4D структуры в 4D пространстве, то ему соответствуют, по крайней мере, одна ее высокосимметричная проекция на 3D пространстве и одна высокосимметричная развертка ее 3D «поверхности» в 3D пространстве.
В связи с этим предположением по высокосимметричному проективному изображению и симметричным производным от развертки гиперячейки 4D структуры в 3D пространстве может быть получена одна и только одна 4D структура с соответствующими топологическими характеристиками.
Предположение 2. Для любой гиперячейки 4D структуры существуют (5-i) различных видов симметричных (4-i)D сечений и (4-i) различных видов симметричных (3-i)D сечений развертки ее 3D «поверхности», где i < 3.
В этом случае по изображениям (4-i)D сечений развертки «поверхности» 4D структуры может быть однозначно идентифицирован прообраз – симметричная развертка «поверхности» в 3D пространстве, а по изображениям (5-i) различных видов симметричных сечений может быть восстановлен соответствующий прообраз – изображение 4D структуры.
Отметим определенный изоморфизм между симметричными сечениями симметричных разверток куба и гиперкуба (рис.1, фрагменты серий 1 и 2). С учетом этого в качестве примера далее будем рассматривать возможные соотношения между геометрико-топологическими свойствами кубических ячеек структурированных 3D и 4D пространств.
Гиперкуб является одним из семи известных автомодулярных политопов 4D пространства, т.к. состоит из восьми топологически одинаковых кубических ячеек: НС-<16, 32, 24, 8>{С8} [5]. Все его геометрические образы, полученные с помощью определенных топологических преобразований в 3D пространстве, обладают дополнительными по сравнению с кубом геометрическими элементами и могут быть использованы при интерпретации нестандартных конфигураций, описывающих ближний порядок в структурах некоторых координационных соединений, особенности стереохимии некоторых молекул органических и металлорганических соединений и другие структурные аномалии. [4, 6-10].
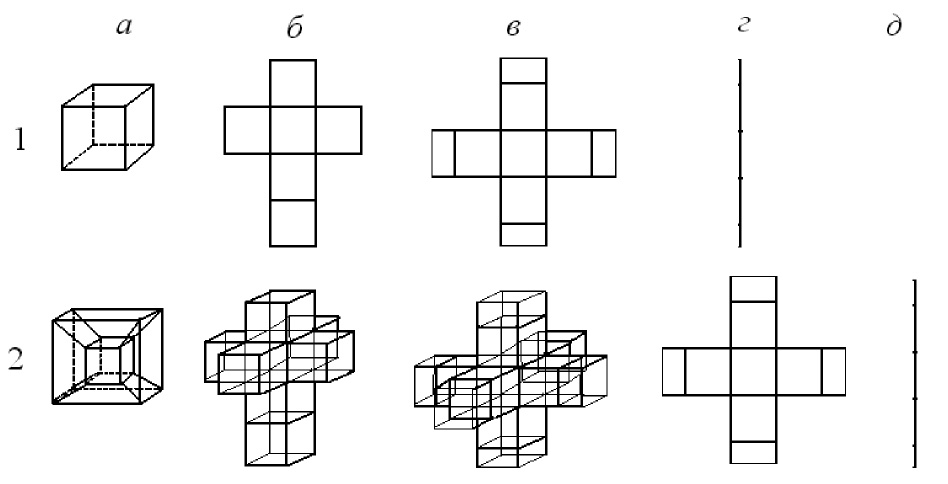
Рис.1. Изображения кубических ячеек (а), их асимметричных и симметричных разверток (б, в) и сечений (г, д) для куба (1) и гиперкуба (2)
Геометрический образ, соответствующий гиперкубу НС – куб внутри куба
С(С)-<8+8, 12+12, 6+6> (с симметрией Оh). Для получения других вероятных геометрических образов из симплекса в 3D пространстве можно воспользоваться результатами его топологических преобразований. При описании топологических преобразований гиперячеек использовали следующий вид символьного представления симплекса и его возможных топологических производных: HPh – <Nv, Ne, Nf, Nph>{Nph рhi}. Данное представление гиперполиэдра содержат информацию о его наименовании (HPh), количестве вершин (v), ребер (e), граней (f), а также количестве и типе ячеек-полиэдров (рh) [11,14].
Рассмотрим топологические преобразования гиперкуба в предположении, что каждая его ячейка, прилегающая к оболочке, подчиняется правилам геометрико-топологических преобразований в 3D пространстве. Известные топологические преобразования куба [1]:
куб {444} → усеченный куб {388} →кубооктаэдр {3434} → усеченный октаэдр {466} → октаэдр {3333}
в используемых здесь обозначениях могут быть представлены в виде следующей цепочки:
C-<8,12,6>{{4}6} → tC-<24,36,14>}{{3}8{8}6} →
CO-<12,24,14> {{3}8{4}6} → tO-<24,36,14>{{6}8{4}6} → O-<6,12,8>{{3}8}.
По аналогии, можно ввести следующие обозначения для изменяющихся оболочек гиперполиэдра: усеченный куб
tC(С)-<32,68,56,16>{tC С T8 tOpyr6}, кубооктаэдр CO(С)-<20,60,64,16>{CO C T8 Tap6}, усеченный октаэдр
tO(С)-<32,80,68,28> {tO C Hpyr8 T12 Hap6},
октаэдр O(С)–<14,48,54,28>{O C Tpyr6 T20}. Здесь и далее конфигурации всех ячеек гиперполиэдров и их вершинная топология представлены в фигурных { } и угловых < > скобках, соответственно. Буквенные обозначения t, p, ap, pyr приведены по первым буквам соответствующих терминов (truncated, prism, anti-prism, pyramid).
Для каждой гиперячейки можно воспользоваться следующими топологическими преобразованиями оболочек их наиболее симметричных проекций в 3D пространстве [11].
1. Сплиттинг-преобразования вершин гиперячейки. Суть преобразования заключается в расщеплении по определенному закону вершин гиперячейки, принадлежащих ее оболочке. Преобразование сопровождается изменением конфигурации оболочки гиперячейки, изменениями числа ребер, количества и формы граней и ячеек.
2. Стелейшн-дизайн внешних граней гиперячейки. Преобразование внешних граней гиперячейки связано с их наращиванием до превращения в вершины новой ячейки.
3. Стретч-оупен-дизайн гиперячейки. Преобразование открытия гиперячейки, сопровождающееся вытягиванием внутренних вершин наружу через одну из граней оболочки.
4. Преобразование Вороного-Дирихле. Преобразование геометрического образа гиперячейки в дуальный ему образ за счет превращения геометрических центров ячеек в вершины, а граней – в ребра [1].
Геометрические образы фрагментов модулярных ячеек в 3D пространстве, полученные в результате описанных выше целенаправленных преобразований симметричных проекций гиперячеек [38-42], формально могут содержать те дополнительные конфигурационные элементы, которые определяют их нестандартность по отношению к общеизвестным координациям атомов в структурах веществ.
Результаты работы получены при поддержке Минобрнауки РФ в рамках государственного задания на проведение НИОКР, шифр заявки N6.8604.2013.
Библиографическая ссылка
Иванов В.В., Таланов В.М. СПОСОБЫ ИДЕНТИФИКАЦИИ ОБРАЗА ГИПЕРКУБИЧЕСКОЙ Р-ЯЧЕЙКИ 4D СТРУКТУРЫ И ДОПУСТИМЫЕ ТОПОЛОГИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ОБОЛОЧЕК ЕЕ НАИБОЛЕЕ СИММЕТРИЧНЫХ 3D ПРОЕКЦИЙ // Современные наукоемкие технологии. 2013. № 12. С. 49-52;URL: https://top-technologies.ru/ru/article/view?id=33594 (дата обращения: 06.02.2026).



