Выделение объектов защиты от вибраций и ударов, в определенной степени, совпадает с технологиями формирования систем автоматического управления, то есть выбором объекта управления, его входных и выходных сигналов с последующей оценкой динамических свойств систем и определением близости параметров динамического состояния заданным [5, 6].
Обеспечение надежности работы машин, связано с детализацией представлений о динамических процессах, в которых формируются нагрузки на узлы и детали машин, что приводит к необходимости разработки подходов и методов определения динамических реакций и усилий, возникающих в динамических взаимодействиях механических колебательных систем [7]. В этом плане заслуживает внимания развитие некоторых методологических позиций в теории виброзащиты, связанных с дополнением известных приемов [2] возможностями, предоставляемыми использованием структурных представлений. Последнее понимается в том смысле, что механическая колебательная система, являющаяся, к примеру, расчетной схемой виброзащитной системы, может быть интерпретирована структурной схемой эквивалентной в динамическом отношении системой автоматического управления [3].
I. Общие положения. Постановка задачи исследования
В простейшем случае объект защиты является твердым телом (материальная точка) с массой m, то есть связь с окружающей средой реализуется через некоторые элементы, или их блоки, которые можно представить как некоторое виброзащитное устройство (рис. 1а,б), располагающееся между источником внешнего возмущения и объектом защиты. При всем разнообразии форм внешнего вибрационного воздействия, чаще всего рассматриваются силовые (рис. 1а) и кинематические (рис. 1б) возмущения [2]. Вибрационное устройство (ВЗУ) может состоять из одного упругого элемента (пружины), приобретать вид некоторого блока из нескольких типовых элементов расширенного набора [3]. Важным условием в формировании ВЗУ является обязательное наличие упругого элемента, принимающего на себя статическую нагрузку. При этом предполагается, что ВЗУ может быть достаточно сложным по своей структуре, и в частности, представлять собой механическую цепь. Структура ВЗУ имеет существенное значение в формировании реакций R и R′, возникающих (рис. 1) в контакте между ВЗУ и объектом защиты, а также между ВЗУ и опорными поверхностями.
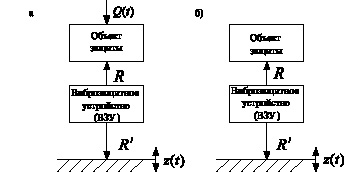
Рис. 1. Принципиальная схема виброзащитной системы:
а – при силовом возмущении; б – при кинематическом возмущении
Задача исследования заключается в оценке возможностей определения динамических реакций в виброзащитной системе, состоящей из объекта защиты, ВЗУ и опорных поверхностей, при учете различных факторов, таких как форма внешнего воздействия, сложности структуры виброзащитного устройства и особенности связей объекта защиты с опорными поверхностями.
II. Особенности формирования математических моделей для оценки динамических реакций
Определение динамических реакций, как следует из постановки задачи, зависит от конкретных реализаций виброзащитной системы. Рассмотрим в качестве примера механическую систему с одной степеью свободы (рис. 2), на которую действуют сила Q, приложенная к массе m и кинематическое возмущение от основания (или опорной поверхности). Виброзащитное устройство состоит из упругого элемента жесткостью k и демпфера вязкого трения с коэффициентом вязкости b. Движение рассматривается в неподвижной системе координат (y). Полагаем, что под действием внешних сил (учитывается действие одного фактора Q ≠ 0, z(t) = 0 или Q = 0, z(t) ≠ 0) объект совершает малые колебания,
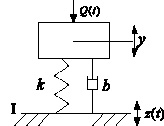
Рис. 2. Виброзащитная система с одной степенью свободы
Пусть Q ≠ 0, z(t) = 0, тогда в соответствии с принципом Даламбера можно записать, что сумма всех сил, действующих на массу m, будет равна нулю. Такая система сил, по определению состоит из силы инерции 
, внешней силы Q (она известна) и силы реакции связей
. (1)
Из (1) следует, что динамическая реакция зависит от величины коэффициента вязкого трения b, что определяет характер движения, которое имеет особенности при докритическом, критическом и закритическом его значении. Если принять, что
, (2)
а частота собственных колебаний определяется
, (3)
то вводя понятия об относительном демпфировании
, (4)
получим, что критический случай соответствует n′ = 1. Принимая внешнюю силу
, (5)
найдем, что динамическая реакция имеет вид
. (6)
Таким образом, при Q ≠ 0, z(t) = 0 сила, передаваемая от объекта к опорной поверхности, будет определяться выражением (6). Динамическая реакция при этом будет передаваться и на объект, а R = R′, то есть в данном случае действие – равняется противодействию. Однако, такая ситуация сохраняется только для тех случаев, когда ВЗУ, взятое само по себе, не обладает своими степенями свободы движения. То есть наличие ВЗУ не должно увеличивать число степеней свободы объекта защиты. Динамическая реакция, в соответствии с (6) может принимать различные значения и при ω → ∞ стремится к нулю. При этом статическая компонента общей реакции остается неизменной. Приведенное выше можно рассматривать как прием определения динамической реакции на основе принципа Даламбера, постулируя динамическую реакцию как компоненту уравнения кинетостатики, связанную с параметрами элементов ВЗУ
(в данном случае k и b). Если периодическая сила является гармонической, то реакция на объекте защиты y может быть найдена подстановкой в (1) значения координаты вынужденных колебаний. Отметим, что отношение модуля динамической реакции к амплитуде внешней силы
(7)
имеет общепринятое название коэффициента виброизоляции [2].
III. Структурные подходы к определению динамических реакций
Виброзащитная система на рис. 2 при условии Q ≠ 0, z(t) = 0, имеет математическую модель в виде дифференциального уравнения
, (8)
которое при использовании преобразований Лапласа приводится к алгебраическоой форме
, (9)
где p = jω 
– комплексная переменная; 
– изображение функций по Лапласу [4,5]. Передаточная функция системы (рис. 2) при входном сигнале 
и выходном 
может быть записана в виде:
. (10)
Полагая, что в операторной форме
, (11)
найдем, что
. (12)
Используя (12) при p = jω, можно найти амплитудно-частотную характеристику, которая совпадает с выражением (7), если принять что b/m = 2n, а 
. Уравнению (9) соответствует структурная схема, приведенная на рис. 3а (построение структурных схем подробно разобрано в [6, 7]). Прямая цепь в структурной схеме содержит звено с передаточной функцией
. (13)
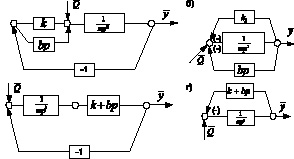
Рис. 3. Структурные схемы виброзащитной системы на рис. 2:
а – схема общего вида; б – схема с выделением звена, соответствующего объекту защиты; в – выделение блока ВЗУ с выходным сигналом ; г – структурная схема для определения приведенного коэффициента жесткости
Это звено по физическому смыслу является приведенной (или обобщенной) пружиной, коэффициент жесткости которой зависит от частоты [3]. В прямой цепи также имеется и «базовое» звено, в динамическом отношении отражающее свойства объекта защиты. На структурной схеме (рис. 3а) показан входной сигнал – сила 
и выходной – смещение объекта по координате 
. Поскольку сила Q прикладывается к массе m, то схема
на рис. 3а может быть преобразована к виду, как показано на рис. 3в, откуда легко определяется
, (14)
тогда
. (15)
В свою очередь, структурная схема на Рис. 3а может быть преобразована к виду, приведенному на Рис. 3б и на рис. 3г. То есть объект защиты (звено с передаточной функцией 1/mp2), имеет обратную отрицательную связь (звено, соответствующее приведенной или обобщенной пружине) с передаточной функцией (13). Физический смысл (13) заключается в том, что обратная свзь соответствует коэффициенту приведенной жесткости ВЗУ. Динамическая реакция в этом случае определится
,
откуда легко получаются выражения (12) и (14). Таким образом определение динамических реакций на основе использования структурных схем, сводится к определению параметров обратной связи, охватывающей звено – объект защиты и иемющее передаточную функцию
(16)
Отметим, что при использовании выражений для передаточных функций начальные условия принимаются равными нулю, что предполагает полное затухание всех переходных процессов. Что касается равенства R = R′, то оно также соблюдается, поскольку механическая цепь (ВЗУ) не имеет своих собственных степеней свободы.
IV. Учет особенностей кинематического возмущения и закрепления объектов защиты
При кинематическом возмущении принимается, что Q = 0, а z(t) ≠ 0, тогда уравнение (9) примет вид
. (17)
Уравнение (17) соответствует структурная схема, приведенная на рис. 4а.
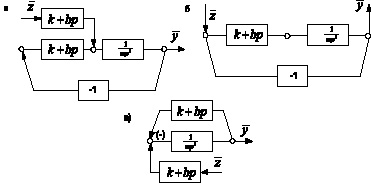
Рис. 4. Структурные схемы виброзащитной системы при кинематическом возмущении:
а – схема в общем виде (при отдельном канале возмущения по z); б – приведенная схема кинематического воздействия; в – структурная схема с выделением обратной связи
Как это следует из рис. 4а, кинематическое воздействие формально приводится к силовому возмущению. Можно записать эквивалентные соотношения в виде
. (18)
Передаточная функция системы на
рис. 4а, имеет вид
,
что совпадает с выражением (10). Если определить передаточную функцию для динамической реакции по возмущению 
(по схеме на рис. 4б), то
, (19)
что совпадает с (12). При этом (19) соответствует, в физическом смысле, коэффициенту виброзащиты [2]. Что касается передаточной функции от смещения 
на динамическую реакцию, то из структурной схемы на рис. 4в следует
. (20)
Если принять во внимание, что кинематическое возмущение 
приводится к эквивалентному силовому воздействию 
, то (20) преобразуется к виду (12), (14)
. (21)
Отметим, что передаточная функция при силовуом входе и динамической реакции на выходе, то есть коэффициент виброизоляции (14) (динамический коэффициент) совпадает с коэффициентом виброзащиты (19), что отмечалось, в частности, в работе [2].
При постановке объекта на опорную поверхность I (рис. 1), возникающие реакции R и R′ равны между собой, что связано с особенностями структуры ВЗУ. Однако в ряде случаев возможны и такие формы виброзащитных систем, когда объект защиты имеет и дополнительные опорные поверхности, как показано на рис. 5 а,б. В этом случае уравнение движения в операторной форме имеет вид
. (22)
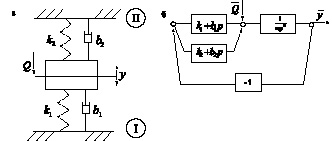
Рис. 5. Расчетная (а) и структурная схема виброзащитной системы с двумя опорными поверхностями (I и II)
Принимая приведенные выше приемы определения динамических реакций, найдем, что
, (23)
, (24)
где 
определяется из передаточной функции, построенной из схемы на рис. 5б:
. (25)
Для определения динамической реакции на элементе m, преобразуем структурную схему на рис. 5 б и получим, что коэффициент жесткости обобщенной пружины составит
, (26)
а динамическая реакция 
имеет вид
. (27)
Аналогичным образом могут быть найдены динамические реакции при кинематических воздействиях, формируемых вибрациями оснований.
Заключение. На основе проведенных исследований можно утверждать, что динамические реакции в виброзащитных системах, рассматриваемых в виде механических колебательных систем, формируются в рамках структурного подхода на основе выделения обратной связи. Такая связь охватывает звено с передаточной функцией интегрирующего элемента второго порядка. При этом физическией смысл передаточной функции обратной (отрицательной в рассматриваемом случае) связи, заключается в том, что она отражает приведенную жесткость обобщенной пружины. В свою очередь, обобщенные пружины могут иметь достаточно сложную структуру, однако, в целом, эта обратная связь не должна иметь своих собственных степеней подвижности. В противном случае нарушается симметрия динамических реакций.
Предлагаемый метод может быть распространен на системы с несколькими степенями свободы; при этом в ВЗУ условие R = R′ в общем случае уже не будет выполняться.
Исследования выполнены по гранту в рамках федеральной целевой программы «Научные и педагогические кадры инновационной России» на 2012 – 2013 гг. (мероприятие 1.3.2. – естественные науки) № 14.132.21.1362.
Библиографическая ссылка
Большаков Р.С., Ермошенко Ю.В., Ковыршин С.В. СТРУКТУРНОЕ МОДЕЛИРОВАНИЕ В ОПРЕДЕЛЕНИИ ДИНАМИЧЕСКИХ РЕАКЦИЙ В ЗАДАЧАХ ВИБРАЦИОННОЙ ЗАЩИТЫ // Современные наукоемкие технологии. – 2013. – № 12. – С. 11-16;URL: https://top-technologies.ru/ru/article/view?id=33588 (дата обращения: 21.11.2024).