Пифагоровы тройки представляют собой когорту из трех целых чисел, удовлетворяющих соотношению Пифагора x2 + y2 = z2. Вообще говоря, это частный случай Диофантовых уравнений, а именно, системы уравнений, в которых число неизвестных больше, чем число уравнений [5]. Известны они давно, еще со времён Вавилона, то есть, задолго до Пифагора. А название они приобрели после того, как Пифагор на их основе доказал свою знаменитую теорему. Однако, как следует из анализа многочисленных источников, в которых вопрос о пифагоровых тройках в той или иной мере затрагивается [1, 2, 4, 5] до сих пор не раскрыт в полной мере вопрос о существующих классах этих троек и о возможных способах их формирования.
Так в книге Саймона Сингха [4] говорится: – «Ученики и последователи Пифагора …поведали миру секрет нахождения так называемых пифагоровых троек.». Однако, в след за этим читаем: – «Пифагорейцы мечтали найти и другие пифагорейские тройки, другие квадраты, из которых можно было бы сложить третий квадрат больших размеров. …По мере того, как числа возрастают, пифагоровы тройки встречаются все реже, и находить их становится все труднее и труднее. Пифагорейцы изобрели метод отыскания таких троек и, пользуясь им, доказали, что пифагоровых троек существует бесконечно много».
В приведенной цитате выделены слова вызывающие недоумение. Почему «Пифагорейцы мечтали найти…», если они «изобрели метод отыскания таких троек…», и почему для больших чисел «находить их становится все труднее и труднее…».
В работе известного математика Д.В. Аносова [1] искомый ответ, вроде бы, приведен. – «Имеются такие тройки натуральных (т. е. целых положительных) чисел x, y, z, что
x2 + y2 = z2. (1)
…можно ли найти все решения уравнения x2+y2=z2 в натуральных числах? …Да. Ответ таков: каждое такое решение можно представить в виде
x=l(m2–n2), y=2lmn, z=l(m2+n2), (2),
где l, m, n – натуральные числа, причем m>n, или в аналогичном виде, в котором x и y меняются местами. Можно чуть короче сказать, что x, y, z из (2) со всевозможными натуральными l и m > n суть все возможные решения (1) с точностью до перестановки x и y. Например, тройка (3, 4, 5) получается при l=1, m=2, n=1. ... По-видимому, вавилоняне знали этот ответ, но как они к нему пришли – неизвестно».
Обычно математики известны своей требовательностью к строгости своих формулировок. Но, в данной цитате такой строгости не наблюдается. Так что именно: найти или представить? Очевидно, что это совершенно разные вещи. Вот ниже приводится строчка «свежеиспеченных» троек (получены методом, описываемым ниже):
12, 35, 37; 20, 21, 29; 44, 117, 125; 103, 5304, 5305.
Не вызывает сомнений, что каждую из этих троек можно представить в виде соотношения (2) и вычислить после этого значения l, m, n. Но, это уже после того, как все значения троек были найдены. А как быть до того?
Нельзя исключить того, что ответы на эти вопросы давно известны. Но их почему-то найти, пока не удалось. Таким образом, целью настоящей работы является системный анализ совокупности известных примеров пифагоровых троек, поиск системообразующих отношений в различных группах троек и выявление системных признаков характерных для этих групп и, затем – разработка простых эффективных алгоритмов расчёта троек с предварительно заданной конфигурацией. Под конфигурацией будем понимать отношения между величинами, входящими в состав тройки.
В качестве инструментария будет использован математический аппарат на уровне, не выходящем за рамки математики, преподаваемой в средней школе, и системный анализ на базе методов, изложенных в [3].
Построение модели
С позиций системного анализа любая пифагорова тройка является системой, образованной объектами, которыми являются три числа и их свойствами. Их совокупность, в которой объекты поставлены в определённые отношения и образуют систему, обладающую новыми свойствами, не присущими ни отдельным объектам, ни любой иной их совокупности, где объекты поставлены в иные отношения.
В уравнении (1), объектами системы являются натуральные числа, связанные простыми алгебраическими соотношениями: слева от знака равенство стоит сумма двух чисел, возведенных в степень 2, справа – третье число, также возведённое в степень 2. Отдельно взятые числа, слева от равенства, будучи возведены в степень 2, не накладывают никаких ограничений на операцию их суммирования – результирующая сумма может быть какой угодно. Но, знак равенства, поставленный после операции суммирования, налагает на значение этой суммы системное ограничение: сумма должна быть таким числом, чтобы результатом операции извлечения корня квадратного явилось натуральное число. А это условие выполняется не для любых чисел, подставляемых в левую часть равенства. Таким образом, знак равенства, поставленный между двумя членами уравнения и третьим, превращает тройку членов в систему. Новым свойством этой системы является введение ограничений на значения исходных чисел.
Исходя из формы записи, пифагорова тройка может рассматриваться как математическая модель геометрической системы, состоящей из трёх квадратов, связанных между собой отношениями суммирования и равенства, как это показано на рис. 1. Рис. 1 является графической моделью рассматриваемой системы, а вербальной её моделью является утверждение:
Площадь квадрата с длиной стороны c может быть разделена без остатка на два квадрата с длинами сторон a и b, таких, что сумма их площадей равна площади исходного квадрата, то есть, все три величины a, b, и c, связаны соотношением
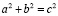. (3)
Графическая модель разложения квадрата
В рамках канонов системного анализа известно, что если математическая модель адекватно отображает свойства некоей геометрической системы, то анализ свойств самой этой системы позволяет уточнить свойства её математической модели, глубже их познать, уточнить, и, при необходимости, усовершенствовать. Этого пути мы и будем придерживаться.
Уточним, что согласно принципам системного анализа операции сложения и вычитания могут производиться только над составными объектами, то есть, объектами, составленными из совокупности элементарных объектов. Поэтому, будем воспринимать любой квадрат, как фигуру, составленную из совокупности элементарных, или единичных квадратов. Тогда условие получения решения в натуральных числах эквивалентно принятия условия, что единичный квадрат неделим.
Единичным квадратом будем называть квадрат, у которого длина каждой из сторон равна единице. То есть, при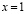 
площадь единичного квадрата определяет следующее выражение.
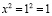(4)
Количественным параметром квадрата является его площадь, определяемая количеством единичных квадратов, которые можно разместить на данной площади. Для квадрата с произвольным значением x, выражение x2 определяет величину площади квадрата, образованного отрезками длиной в x единичных отрезков. На площади этого квадрата могут быть размещены x2 единичных квадратов.
Приведенные определения могут быть восприняты как тривиальные и очевидные, но это не так. Д.Н. Аносов [1] определяет понятие площадь по-другому: – « … площадь фигуры равна сумме площадей ее частей. Почему мы уверены, что это так? …Мы представляем себе фигуру сделанной из какого-то однородного материала, тогда ее площадь пропорциональна количеству содержащегося в ней вещества – ее массе. Далее подразумевается, что когда мы разделяем тело на несколько частей, сумма их масс равна массе исходного тела. Это понятно, потому что все состоит из атомов и молекул, и раз их число не изменилось, то не изменилась и их суммарная масса… Ведь, собственно, масса куска однородного материала пропорциональна его объему; значит, надо знать, что объем «листа», имеющего форму данной фигуры, пропорционален ее площади. Словом, …что площадь фигуры равна сумме площадей ее частей, в геометрии надо это доказывать. … В учебнике Киселева существование площади, имеющей то самое свойство, которое мы сейчас обсуждаем, честно постулировалось как некое допущение, причем говорилось, что это на самом деле верно, но мы этого доказывать не будем. Так что и теорема Пифагора, если ее доказывать с площадями, в чисто логическом отношении останется не совсем доказанной».
Нам представляется, что введенные выше определения единичного квадрата снимают указанную Д.Н. Аносовым неопределенность. Ведь если величина площади квадрата и прямоугольника определяется суммой заполняющих их единичных квадратов, то при разбиении прямоугольника на произвольные, прилегающие друг к другу части площадь прямоугольника естественно равна сумме всех его частей.
Более того, введенные определения снимают неопределенность использования понятий «разделить» и «сложить» применительно к абстрактным геометрическим фигурам. Действительно, что значит разделить прямоугольник или любую другую плоскую фигуру на части? Если это лист бумаги, то его можно разрезать ножницами. Если земельный участок – поставить забор. Комнату – поставить перегородку. А если это нарисованный квадрат? Провести разделительную линию и заявить, что квадрат разделён? Но, ведь говорил Д.И. Менделеев: «…Заявить можно всё, а ты – поди, демонстрируй!»
А при использовании предложенных определений «Разделить фигуру» означает разделить количество заполняющих эту фигуру единичных квадратов на две (или более) частей. Количество единичных квадратов в каждой из таких частей определяет её площадь. Конфигурацию этим частям можно придавать произвольную, но при этом сумма их площадей всегда будет равна площади исходной фигуры. Возможно, специалисты-математики сочтут эти рассуждения некорректными, тогда примем их за допущение. Если уж в учебнике Киселёва приемлемы такие допущения, то и нам подобным приёмом грех не воспользоваться.
Первым этапом системного анализа является выявление проблемной ситуации. В начале этого этапа было просмотрено несколько сот пифагоровых троек, найденных в различных источниках. При этом внимание привлекло то обстоятельство, что всю совокупность пифагоровых троек, упоминающихся в публикациях, можно разделить на несколько групп, различающихся по конфигурации. Признаком специфичной конфигурации будем считать разность длин сторон исходного и вычитаемого квадратов, то есть, величину c–b. Например, в публикациях довольно часто в качестве примера демонстрируются тройки, удовлетворяющие условию c–b=1 [1, 4, 6]. Примем, что вся совокупность таких пифагоровых троек образует множество, которое будем называть «Класс c–1», и проведём анализ свойств этого класса.
Рассмотрим три квадрата, представленные на рисунке, где c – длина стороны уменьшаемого квадрата, b – длина стороны вычитаемого квадрата и a – длина стороны квадрата, образованного из их разности. На рис. 1 видно, что при вычитании из площади уменьшаемого квадрата площади вычитаемого квадрата в остатке остаются две полосы единичных квадратов:
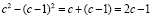. (5)
Для того чтобы из этого остатка можно было образовать квадрат, необходимо выполнение условия
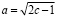. (6)
Эти соотношения позволяют определить значения всех членов тройки по единственному заданному числу c. Наименьшим числом c, удовлетворяющим соотношению (6), является число c = 5. Итак, были определенны длины всех трёх сторон квадратов, удовлетворяющих соотношению (1). Напомним, что значение b стороны среднего квадрата
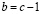(7)
было выбрано, когда мы решили образовать средний квадрат путем уменьшения стороны исходного квадрата на единицу. Тогда из соотношений (5), (6). (7) получаем следующее соотношение:
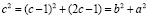, (8)
из которого следует, что выбранное значение c = 5 однозначно задаёт значения b = 4, a = 3.
В итоге, получены соотношения, позволяющие представить любую пифагорову тройку класса «c – 1» в таком виде, где значения все трёх членов определяются по одному задаваемому параметру – значению c:
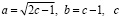. (9)
Добавим, что число 5 в приведенном выше примере появилось как минимальное из всех возможных значений c, при которых уравнение (6) имеет решение в натуральных числах. Следующее число, обладающее таким же свойством, это 13, затем 25, далее 41, 61, 85 и т. д. Как видно, в этом ряду чисел интервалы между соседними числами интенсивно возрастают. Так, например, после допустимого значения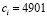 
, следующее допустимое значение 
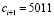, а после 
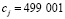, следующее допустимое значение 
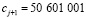, то есть, допустимое значение отстоит от предыдущего более чем на пятьдесят миллионов!
Теперь понятно, откуда появилась эта фраза в книге [4]: – «По мере того, как числа возрастают, пифагоровы тройки встречаются все реже, и находить их становится все труднее и труднее…». Однако это утверждение не является верным. Стоит только взглянуть на пифагоровы тройки, соответствующие приведенным выше парам соседних значений c, как сразу бросается в глаза одна особенность – в обеих парах, в которых значения c разнесены на столь большие интервалы, значения a оказываются соседними нечетными числами. Действительно, для первой пары имеем
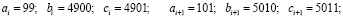
и для второй пары
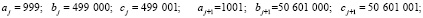
Так что «всё реже встречаются» не сами тройки, а интервалы между соседними значениями c увеличиваются. Сами же пифагоровы тройки, как это будет показано ниже, существуют для любого натурального числа.
Теперь рассмотрим, тройки следующего класса – «Класс c-2». Как видно из рис. 1, при вычитании из квадрата со стороной c квадрата со стороной (c – 2), образуется остаток в виде суммы двух единичных полос. Величина этой суммы определяется уравнением:
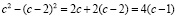(10)
Из уравнения (10) получаем соотношения, определяющее любую из бесконечного множества троек класс «c-2»:
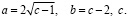(11)
Условием существования решения уравнения (11) в натуральных числах является любое такого значения c , при котором a является натуральным числом. Минимальное значение c, при котором решение существует, составляет c = 5. Тогда «стартовая» тройка для этого класса троек определяется набором a = 4, b = 3, c = 5. То есть, вновь, образуется классическая тройка 3, 4, 5, только теперь площадь вычитаемого квадрата меньше площади остатка.
И наконец, проведём анализ троек класса «с–8». Для этого класса троек при вычитании площади квадрата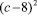 
из площади с2 исходного квадрата, получаем:
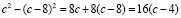. (12)
Тогда, из уравнения (12) следует:
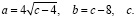(13)
Минимальное значение c, при котором решение существует: это c = 13. Пифагорова тройка при этом значении примет вид 12, 5, 13. В этом случае опять площадь вычитаемого квадрата меньше площади остатка. А переставив обозначения местами, получим тройку 5, 12, 13, которая по своей конфигурации относится к классу «c – 1». Похоже, что дальнейший анализ других возможных конфигураций ничего принципиально нового не откроет.
Вывод расчётных соотношений
В предыдущем разделе логика анализа развивалась в соответствии с требованиями системного анализа по четырём из пяти основных его этапов: анализ проблемной ситуации, формирование целей, формирование функций и формирование структуры. Теперь пора переходить к заключительному, пятому этапу – проверка реализуемости, то есть, проверка того, в какой мере поставленные цели достигнуты. [3].
Ниже показана табл. 1, в которой приведены значения пифагоровых троек, относящихся к классу «c – 1». Большинство троек встречаются в различных публикациях [1, 2, 5, 6], но тройки для значений a, равных 999, 1001 в известных публикациях не встречались.
Таблица 1
Пифагоровы тройки класса «с–1»
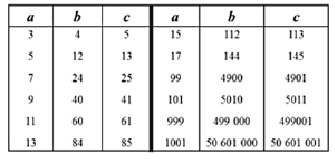
Можно проверить, что все тройки удовлетворяют соотношению (3). Таким образом, одна из поставленных целей достигнута. Полученные в предыдущем разделе соотношения (9), (11), (13) позволяют формировать бесконечное множество троек, задавая единственный параметр c – сторону уменьшаемого квадрата. Это, конечно, более конструктивный вариант, чем соотношение (2), для использования которого следует задать произвольно три числа l, m, n, имеющих любое значение, затем искать решение, зная только, что в итоге, непременно будет получена пифагорова тройка, а какая – заранее неизвестно. В нашем случае заранее известна конфигурация формируемой тройки и нужно задавать только один параметр. Зато, увы, не для каждого значения этого параметра решение существует. И надо заранее знать его допустимые значения. Так что полученный результат хорош, но, далёк от идеала. Желательно получить такое решение, чтобы пифагоровы тройки можно было вычислять для любого произвольно заданного натурального числа. С этой целью вернемся к четвёртому этапу – формирование структуры полученных математических соотношений.
Поскольку выбор величины c в качестве базового параметра для определения остальных членов тройки оказался неудобным, следует испробовать другой вариант. Как видно из табл. 1, выбор параметра a в качестве базового представляется предпочтительным, поскольку значения этого параметра идут подряд в ряду нечётных натуральных чисел. После несложных преобразований приводим соотношения (9) к более конструктивному виду:
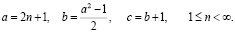(14)
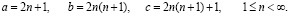(15)
Соотношения (14) позволяют найти пифагорову тройку для любого наперёд заданного нечётного значения a. При этот простота выражения для b позволяет производить вычисления даже без калькулятора. Действительно, выбрав, к примеру, число 13, получаем:
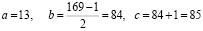. (16)
А для числа 99 соответственно получаем:
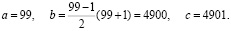(17)
Соотношения (15) позволяют получать значения всех трёх членов пифагоровой троки для любого заданного n, начиная с n=1.
Теперь рассмотрим пифагоровы тройки класса «c – 2». В табл. 2 приведены для примера десять таких троек. Причем, в известных публикациях были найдены только три пары троек – 8, 15, 23; 12, 35, 36; и 16, 63, 65. Этого оказалось достаточно, чтобы определить закономерности, по которым они формируются. Остальные семь были найдены из выведенных ранее соотношений (11). Для удобства вычисление эти соотношения были преобразованы так, чтобы все параметры выражались через величину a. Из (11) с очевидность следует, что все тройки для класса «c – 2» удовлетворяют следующим соотношениям:
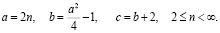(18)
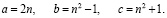(19)
Таблица 2
Пифагоровы тройки класса «с–2»
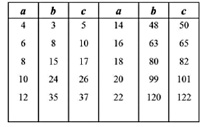
Как видно из табл. 2, всё бесконечное множество троек класса «c – 2» можно разделить на два подкласса. Для троек, у которых значение a делится на 4 без остатка, значения b и c – нечётные. Такие тройки, у которых НОД = 1, называют примитивными [2, 4]. Для троек, у которых значения a не делится на 4 в целых числах, все три члена тройки a, b, c – чётные.
Теперь перейдём к рассмотрению результатов анализа третьего из выделенных классов – класса «c – 8». Расчётные соотношения для этого класса, полученные из (13), имеют вид:
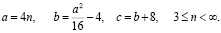(20)
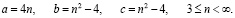(21)
Соотношения (20), (21) по сути, идентичны. Различие только в выборе последовательности действий. Либо, в соответствии с (20) выбирается желательное значение a (в данном случае требуется , чтобы это значение делилось на 4), затем, определяются величины b и c. Либо, выбирается произвольное число , и затем, из соотношений (21) определяются все три члена пифагоровой тройки. В табл. 3 приведен ряд пифагоровых троек, вычисленных указанным способом. Однако, вычислять значения пифагоровых троек можно ещё проще. Если известно хоть одно значение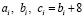 
, то все последующие значения определяются очень просто по следующим соотношениям:
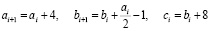(22)
Таблица 3
Пифагоровы тройки класса «с–8»
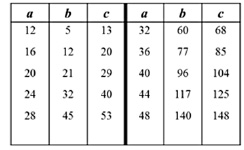
Справедливость соотношения (22) для всех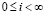 
может быть проверена как по тройкам из табл. 2, так и по другим источникам. В качестве примера, в табл. 4 курсивом выделены тройки из обширной таблицы пифагоровых троек (10000 троек), вычисленных на основе компьютерной программы [5] по соотношению (2) [6] и жирным шрифтом – тройки, вычисленные по соотношения (20). Эти значения в указанной таблице отсутствовали.
Таблица 4
Пифагоровы тройки класса «с–8»
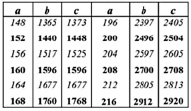
Соответственно, для троек вида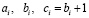 
могут использоваться соотношения:
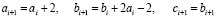(23)
И для троек вида <<besk33.wmf>>, имеем соотношение:
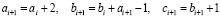(24)
Следует подчеркнуть, что рассмотренные выше классы троек «c – 1», «с – 2», «с – 8» составляют более 90 % среди первой тысячи троек, из таблицы приведенной в [6]. Это даёт основания воспринимать указанные классы как базовые. Добавим, что при выводе соотношений (22), (23), (24) не использовались какие либо специальные свойства чисел, изучаемые в теории чисел (простые, взаимно простые и пр.). Выявленные закономерности формирования пифагоровых троек обусловлены только системными свойствами описываемых этими тройками геометрических фигур – квадратов, состоящих из совокупности единичных квадратов.
Заключение
Теперь, как сказал Эндрю Уайлс в 1993 г.: «Думаю, мне следует на этом остановиться» [4]. Поставленная цель полностью достигнута. Показано, что анализ свойств математических моделей, структура которых связана с геометрическими фигурами, существенно упрощается, если в процессе анализа наряду с чисто математическими выкладками учитываются и геометрические свойства изучаемых моделей. Упрощение достигается, в частности за счёт того, что исследователь «видит» искомые результаты, не проводя математических преобразований.
Например, равенство
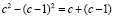
становится очевидным без преобразований в левой его части, стоит только взглянуть на рис. 1, где приведена графическая модель этого равенства.
В итоге, на основе проведенного анализа показано, что для любого квадрата со стороной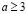 
могут быть найдены квадраты со сторонами b и c, такие, что для них выполняется равенство 
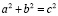и получены соотношения, обеспечивающие получение результатов при минимальном объеме вычислений:
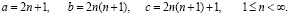
для нечётных значений a,
и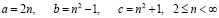 
– для чётных значений.
Библиографическая ссылка
Бескровный И.М. СИСТЕМНЫЙ АНАЛИЗ СВОЙСТВ ПИФАГОРОВЫХ ТРОЕК // Современные наукоемкие технологии. – 2013. – № 11. – С. 135-142;URL: https://top-technologies.ru/ru/article/view?id=33537 (дата обращения: 21.11.2024).