При решении задач преобразования геометрических фигур, таких как сложение и вычитание площадей квадратов, количественные результаты получают из алгебраических выражений, являющимися модельными отображениями этих фигур. При этом следует учитывать, что любая модель отображает лишь ограниченную совокупность свойств, присущих оригиналу [2]. Недостаточный учёт этого фактора может привести к ошибочной интерпретации полученного результата. Пусть, например, выражение
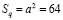 (1)
(1)
обозначает площадь квадрата, длина стороны которого равна a. Можно ли разделить эту площадь пополам, получив целочисленное решение? Известно, что разделить квадрат на два квадрата одинаковой площади в натуральных числах невозможно. А что означает следующее выражение?
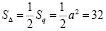 . (2)
. (2)
В данном случае значение 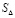 , обозначает площадь треугольника, образованного делением квадрата на две равные части путём проведения диагонали, как это показано на рис. 1. Естественно, проводя длинную цепочку алгебраических преобразований можно не заметить такого качественного изменения исходной фигуры и в итоге получить некорректный результат. Из этого вытекает необходимость постоянного контроля адекватности получаемых алгебраических выражений описываемым геометрическим фигурам. Именно, такой подход был реализован в работе [3], где подробно рассмотрен процесс вычисления пифагоровых троек. Сами по себе триады чисел a, b, c, именуемые пифагоровыми тройками, были известны еще во времена Вавилона [1, 4]. Числа, входящие в пифагоровы тройки, связаны между собой соотношением
, обозначает площадь треугольника, образованного делением квадрата на две равные части путём проведения диагонали, как это показано на рис. 1. Естественно, проводя длинную цепочку алгебраических преобразований можно не заметить такого качественного изменения исходной фигуры и в итоге получить некорректный результат. Из этого вытекает необходимость постоянного контроля адекватности получаемых алгебраических выражений описываемым геометрическим фигурам. Именно, такой подход был реализован в работе [3], где подробно рассмотрен процесс вычисления пифагоровых троек. Сами по себе триады чисел a, b, c, именуемые пифагоровыми тройками, были известны еще во времена Вавилона [1, 4]. Числа, входящие в пифагоровы тройки, связаны между собой соотношением
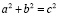 , (3)
, (3)
означающим, что сумма площадей двух квадратов со сторонами a и b равна площади квадрата со стороной c. Пифагоровыми эти тройки названы вследствие того, что Пифагор в своей знаменитой теореме связал эти три числа с катетами и гипотенузой прямоугольного треугольника.
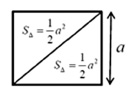
Рис. 1. Деление квадрата
Дополнительный интерес к пифагоровым тройкам был усилен известной теоремой Ферма, утверждающей, что уравнение (3), преобразованное к виду
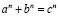 (4)
(4)
не имеет решения при n>2. Ферма сформулировал это утверждение так: «Невозможно для куба быть записанным в виде суммы двух кубов, или для четвертой степени быть записанной в виде суммы двух четвертых степеней, или, в общем, для любого числа, которое есть степень больше двух, быть записанной в виде суммы двух таких же степеней.» [5]. Ферма утверждал: – «Я нашел поистине удивительное доказательство этого предложения, но поля здесь слишком узки для того, чтобы вместить его» [4].
Далее исходя из текста цитаты из прекрасной книги Саймона Сингха: «Великая теорема Ферма стала величайшим вызовом математикам, и тот, кто сумел бы решить проблему Ферма, заслужил бы восторженное поклонение всего математического сообщества. За ее доказательство предлагались призы; процветало соперничество. У Великой теоремы Ферма богатая история, знавшая смерть и мошенничество. Она оказала определенное влияние на развитие математики», [4] становится понятным повышенный интерес к пифагоровым тройкам. Надо отметить – необоснованно завышенный. Дело в том, что лишенная ореола таинственности, навеянного теоремой Ферма, проблема вычисления пифагоровых троек на поверку оказалась весьма простой, чтобы не сказать примитивной.
Использованные в [3] методы системного анализа позволили получить простые расчётные формулы, позволяющие для любого заданного значения вычислить такие значения a и b, которые удовлетворяют соотношению (3).
Так, для нечётных значений
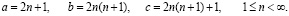 (5)
(5)
для чётных значений
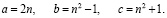
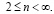 (6)
(6)
Цель настоящей работы – завершить исследование свойств пифагоровых троек, а именно – показать связь этих троек с теоремой Пифагора, а затем применить такой же подход, как и в [3] к исследованию проблемы разделения куба.
А при чём здесь Пифагор?
До этого момента и в работе [3] и в предыдущем тексте настоящей рабы сознательно не приводилось упоминание о треугольниках, чтобы подчеркнуть независимость проблемы разделения квадратов от проблем с углами треугольников. Как было сказано выше и, как показано в [3] задача получения пифагоровых троек, сводится к простой задаче разделения квадрата на две части, которая решается весьма просто безо всякой привязки к теореме Пифагора. В связи с этим и возникает резонный вопрос, а при чём здесь Пифагор? Мы не можем узнать, каким образом Пифагор пришел к своей знаменитой теореме, но один из возможных вариантов можно предположить.
Дело в том, что если что если три квадрата, вычисленные по соотношения (5) или (6) соединить углами так, как это показано на рис. 2, то внутри окажется пространство, являющееся ни чем иным, как прямоугольным треугольником. (Разрывы между углами оставлены для наглядности) В соответствии с этим, можно сформулировать теорему, которую можно назвать обратной теоремой Пифагора.
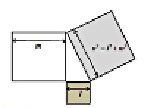
Рис. 2. Образование прямоугольного треугольника
Обратная теорема Пифагора. Любые три квадрата из триад, вычисленных по соотношениям (5), (6), соединенные своими углами, образуют замкнутое пространство, являющееся прямоугольным треугольником.
Доказательство: Из тригонометрии известно, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Для треугольника, образованного соединением углов трех квадратов, связанных соотношением 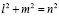 , квадрат гипотенузы равен сумме квадратов катетов. Значит, этот треугольник прямоугольный по построению.
, квадрат гипотенузы равен сумме квадратов катетов. Значит, этот треугольник прямоугольный по построению.
Теперь, разобравшись порядком с квадратами, резонно испробовать эффективность предложенного подхода на кубе. Иными словами – А не замахнуться ли нам на самого великого Ферма? (Перефраз из к.ф «Берегись автомобиля»)
К теореме Ферма нас ведёт проблема разделения куба на два куба. Профессиональным математикам и любителям, занимавшимся теоремой Ферма, знают, что стоит доказать несправедливость теоремы хотя бы для одного показателя степени не равного двум, и теорема будет опровергнута. Мы не собираемся опровергать великую теорему. И не собираемся её доказывать. Теорема верна, даже более чем верна, и не потому только, что считается доказанной [4]. Просто утверждение, в ней содержащееся, является достаточно тривиальным.
Попробуем показать это на проблеме разделения куба. Итак, наша цель показать, что решения уравнения
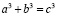 (7)
(7)
не существует просто в силу присущих кубу системных свойств, как объекту трёхмерного мира,
Для начала познакомимся с двумя цитатами из книги Сингха: «Во всех моих беседах с математиками меня поражала необычайная точность, с которой они выражали свои мысли» И далее – «...математики просто терпеть не могут высказывать ложные утверждения. Разумеется, они используют интуицию и не чужды вдохновения, но формальные суждения должны быть логически безупречными» [4].
Прекрасная, весьма похвальная привычка, достойная постоянного подражания. Но как это согласовать с таким высказыванием: «Вместо уравнения Пифагора x2 + y2 = z2 Ферма занялся рассмотрением его варианта x3 + y3 = z3. Ферма всего лишь изменил степень на единицу, но его новое уравнение, насколько можно было судить, вообще не допускало никаких решений в целых числах. «Методом проб и ошибок» нетрудно было обнаружить, что найти два куба, которые бы в сумме давали еще один куб, не так-то просто. Неужели произведенное Ферма незначительное изменение действительно превращает уравнение, допускающее бесконечно много решений в целых числах, в уравнение, не имеющее ни одного решения в целых числах?» (Фрагменты выделены нами).
Да уж, ничего себе необычайная точность и логически безупречные суждения. Разве можно считать переход от двухмерного, плоского пространства, в котором рассматривается проблема разделения квадратов к трёхмерному объемному пространству, в котором надлежит рассматривать проблему разделения кубов незначительным изменением? И, не обращая внимания на кардинальное изменение условий задачи, пытаться бездумно перенести закономерности двухмерного пространства в трёхмерное?
Ну да, изменил степень лишь на единицу. Вот уж действительно по Маяковскому: – «Единица – вздор, единица – ноль, …» В. Маяковский. «Владимир Ильич Ленин». Но, то была поэзия, а здесь – математика. Вопрос – какая математика? Абстрактная, которая не интересуется, какие объекты она описывает, и описывает ли вообще? А вместо какого-то «скучного моделирования» занимается просто манипуляциями с числами. Или всё-таки существует специфика, которую следует учитывать при анализе геометрических фигур. Трудно сказать, задумывался ли об этом Ферма. Во всяком случае, его формулировка теоремы: «Невозможно для куба быть записанным в виде суммы двух кубов, или для четвертой степени быть записанной в виде суммы двух четвертых степеней, или, в общем, для любого числа, которое есть степень больше двух, быть записанной в виде суммы двух таких же степеней. (лат.)» ([5]) – звучит так, как будто речь идёт просто о показателе степени n=3, именуемой кубом, а не о геометрической фигуре.
Однако поскольку исходная проблема возникла из области геометрии, а именно из теоремы Пифагора, то в настоящей работе, так же как и в предшествующей [3], рассматриваются не проблемы теории чисел, а исключительно проблемы анализа геометрических фигур.
В таком случае изменение показателя степени на единицу имеет кардинальное значение. При n =1 имеем одномерное линейное пространство. Здесь мы от любого отрезка можем за один акт деления отделять (или присоединять) одну часть произвольной длины. При n=2 переходим в двухмерное пространство. Здесь размеры квадратов при разделении или сложении изменяются в двух измерениях – в длину и высоту. И это накладывает дополнительные ограничения. Квадрат, как оказывается, можно разделить на два квадрата. Но, не любой квадрат, и не на произвольные части, а лишь при соблюдении присущих двухмерному пространству закономерностей.
А при n=3 переходим в трёхмерное пространство. Здесь геометрические фигуры трансформируются в трёх измерениях – длина, ширина и высота. И это обстоятельство накладывает дополнительные ограничения на возможности разделения и сложения геометрических фигур. Рассмотрим это подробнее на примере куба, используя тот же подход, который использовался в [3] при анализе квадратов. Эта процедура иллюстрируется на рис.3.
Как видно из рис. 3, при выделении квадрата (c-1)2 из квадрата со стороной c2 остаток составляют две полосы единичных квадратов: справа отделяется полоса из c единичных квадратов и сверху ещё полоса из c-1 единичных квадратов. Очевидно, что для того, чтобы сформировать из этого остатка квадрат, со стороной c-2 требуется выполнение равенства
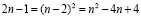 . (8)
. (8)
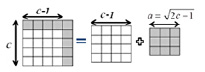
Рис. 3. Графическая модель разложения квадрата
Из равенства (8) следует квадратное уравнение вида
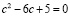 , (9)
, (9)
решениями которого являются два значения: 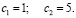 Это ещё один вариант доказательства давно известной истины существования квадратов, площадь которых равна сумме площадей двух квадратов. И, дополнительно, один из вариантов нахождения таких квадратов. В данном случае полученное решение соответствует известной пифагоровой тройке 3, 4, 5.
Это ещё один вариант доказательства давно известной истины существования квадратов, площадь которых равна сумме площадей двух квадратов. И, дополнительно, один из вариантов нахождения таких квадратов. В данном случае полученное решение соответствует известной пифагоровой тройке 3, 4, 5.
Теперь перейдём к анализу куба. Здесь требуется одно дополнительное уточнение. Если при анализе квадратов единицей площади являлся единичный квадрат, то при анализе проблем разделения и суммирования объемов кубов неделимой единицей объема является единичный куб, объём которого равен 1.
Процедуру разделения куба иллюстрируется на рис. 4, из которого видно, что при выделении куба с ребром, равным n-1 из куба с ребром, равным n, образуется остаток, состоящий из трёх частей. Справа отделяется квадратная пластина, содержащая 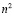 единичных кубов, сверху снимается пластина, содержащая
единичных кубов, сверху снимается пластина, содержащая 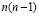 единичных кубов, и сзади снимается квадратная пластина, содержащая
единичных кубов, и сзади снимается квадратная пластина, содержащая 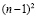 единичных кубов. Таким образом, остаток определяется выражением
единичных кубов. Таким образом, остаток определяется выражением
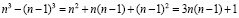 . (10)
. (10)
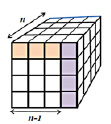
Рис. 4. Разделение куба
Соответственно, для того, чтобы из этого остатка можно было сформировать куб с ребром, равным n-2, требуется выполнение равенства
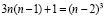 . (11)
. (11)
Из (11) следует кубическое уравнение
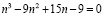 , (12)
, (12)
в решении которого содержится один действительный, но не целочисленный, и два комплексно-сопряжённых корня:
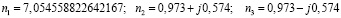 .
.
|
Куб |
Длина ребра |
Объём |
Сумма l3+ k3 |
|
n3 |
7,054559 |
351,0828 |
351,0828 |
|
l3 |
6,054559 |
221,9461 |
|
|
m3 |
5,054559 |
129,0828 |
Тот факт, что уравнение не имеет целочисленного решения, означает, что объем куба можно разделить на два куба, но не в натуральных числах. В итоге была получена своеобразная «тройка Ферма», о которой он мечтал (Ферма мечтал получить тройку чисел для степени с показателем n>2 [4]): 5,054559, 6,054559, 7, 0545559. Выписывание семи знаков после запятой здесь необходимо для того, чтобы точно выполнялось равенство суммы двух полученных кубов величине исходного куба. В табл. 1 приведены сводные данные по этим кубам.
Чтобы посмотреть, а что получается при попытке найти решение в натуральных числах, можно взять тройку натуральных чисел, ближайших по значению к числам, приведенным в таблице. Перейдя к рациональным числам 5, 6, 7, получим тройку кубов 125, 216, 343. Однако в этой тройке сумма двух первых кубов меньше величины третьего куба на два единичных куба: 125+216=341. Добавив в левую часть два единичных куба с ребром k=1, получаем следующее соотношение:
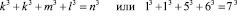 (13)
(13)
В данном случае куб с ребром, равным 7, поддался разделению на четыре куба. Однако, это количество не является при разделении кубов минимальным. Дальнейший анализ показывает, что любой куб может быть разделён на несколько кубов, но, для решений в натуральных числах число этих кубов будет всегда больше двух. Минимальное число, на которое можно разделить куб, равно трём. При экспериментальной проверке этого утверждения установлено, что в диапазоне первых трёх сотен числового ряда достаточно регулярно наблюдается соблюдение следующего равенства:
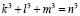 (14)
(14)
В итоге, в указанном диапазоне натуральных чисел было выявлено 10 таких четвёрок чисел 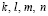 , которые в дальнейшем будем называть квадригами.
, которые в дальнейшем будем называть квадригами.
Первая сотня Вторая сотня Третья сотня
3, 4, 5, 6 12, 31, 102, 103 4, 51, 213, 214
1, 6, 8, 9 3, 34, 114, 115 4, 57, 248, 249
3, 10, 18, 19 9, 58, 255, 256
2, 17, 40, 41 15, 64, 297, 298
Достаточная регулярность появления квадриг даёт веские основания считать этот факт системным свойством трехмерных структур. А далее, на основании этого факта и с учётом системных свойств, выявленных при анализе проблемы разделения двухмерных фигур – квадратов, можно сформулировать следующий постулат:
Минимальное количество частей Qmin, на которое может быть разделена геометрическая фигура, описываемая выражением 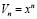 , определяется неравенством
, определяется неравенством 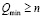 . Квадрат, со стороной z может быть разделён минимум на два квадрата со сторонами x, y. Эти числа связаны соотношением
. Квадрат, со стороной z может быть разделён минимум на два квадрата со сторонами x, y. Эти числа связаны соотношением 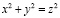 . Куб с ребром n может быть разделён минимум на три куба с рёбрами k, l, m, которые связаны соотношением
. Куб с ребром n может быть разделён минимум на три куба с рёбрами k, l, m, которые связаны соотношением 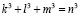 . Соответственно, объект, описываемый четвёртой степенью, может быть разделён минимум на четыре части. и т.д.
. Соответственно, объект, описываемый четвёртой степенью, может быть разделён минимум на четыре части. и т.д.
Условия, при которых обеспечивается справедливость соотношений типа (7), (14) и подобных им, специфичны для каждого класса геометрических фигур и зависят, в первую очередь, от размерности пространства, в котором реализована фигура. Попытки поиска закономерностей присущих пространству с определённой размерностью при анализе фигур другой размерности противоречат системной сущности геометрических объектов и потому безрезультатны. При этом безрезультатность подобных попыток в дополнительных математических доказательствах не нуждается.
Заключение
В работе был продолжен системный анализ проблем разделения квадрата на два целых квадрата и вычисления пифагоровых троек. Дополнительно к известному доказательству формирования таких троек на основе теоремы Пифагора, выведено уравнение (9), математически доказывающее возможность разделения квадрата на два квадрата, поскольку решение этого уравнения содержит два целочисленных корня.
Установлено, что при соединении углов трёх квадратов, одного исходного и двух производных, образующихся при делении, внутри соединённых квадратов образуется пространство, являющееся прямоугольным треугольником. Возможно, что формулировку этого утверждения можно считать обратной теоремой Пифагора.
Рассмотрена проблема разделения куба на два куба, по аналогии с известной процедурой разделения квадратов, как это сформулировано в теореме Ферма. Выведено кубическое уравнение (12), характер корней которого является критерием возможности реализации такой процедуры. Решение этого уравнения содержит один действительный корень оказавшийся не целочисленным, и два – комплексно-сопряженных. Отсутствие рационального корня доказывает, что разделить куб на два куб невозможно. Этот факт можно было бы считать одним из доказательств теоремы Ферма, однако, теорема здесь не причём. Просто куб, в силу присущих ему, как объекту трехмерного пространства, системных свойств, делится не на две, а на три части. При этом в результате деления образуются четыре куба – один исходный и три – производных. Ребра этих кубов 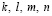 образуют четверку, названную квадригой, все члены которой связаны между соотношением
образуют четверку, названную квадригой, все члены которой связаны между соотношением 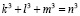 .
.
Анализ, проведенный в диапазоне первых трёх сотен числового ряда, выявил наличие десяти таких квадриг. Установить закономерность их появления от величины n пока не удалось. Однако сам факт, что минимальное количество кубов, на которые можно разделить исходный куб, равно трём, можно считать доказанным. Отсюда следует, что распространение области действия теоремы Ферма на показатель степени 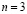 является избыточным. Куб просто не делится на два целых куба столь же естественно, как например, девять не делится на два. И этот факт не требует никаких математических доказательств.
является избыточным. Куб просто не делится на два целых куба столь же естественно, как например, девять не делится на два. И этот факт не требует никаких математических доказательств.
Библиографическая ссылка
Бескровный И.М. АЛГЕБРА ГЕОМЕТРИЧЕСКИХ ФИГУР И ГЕОМЕТРИЯ АЛГЕБРАИЧЕСКИХ ФОРМУЛ // Современные наукоемкие технологии. 2013. № 11. С. 129-134;URL: https://top-technologies.ru/ru/article/view?id=33536 (дата обращения: 04.03.2026).



