Пусть имеется n различных товаров. Обозначим некоторый набор товаров n-мерным вектором.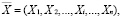 
где 
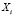– количество i-го товара в наборе.
Считается, что любой потребитель может сказать о двух произвольных наборах, какой из них ему наиболее желателен или что он не видит разницу между наборами. Примем, что на множестве потребительских наборов определена функция
.
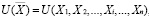Такая функция называется функцией полезности потребителя, или функцией потребительского предпочтения.
В прикладных задачах и моделях потребительского выбора часто используется частный случай набора из двух товаров. При этом вводится понятие кривой безразличия, под которой понимается кривая, соединяющая потребительские наборы с одним и тем же уравнением удовлетворения потребностей индивида.
В теории потребления предполагается, что потребитель всегда стремиться максимизировать свою полезность и ограничением для него является величина дохода I, которую он может потратить на приобретение набора товаров.
Задачу потребительского выбора рассмотрим для случая наборов из двух товаров: найти такой набор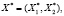 
для которого 
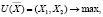при ограничениях: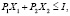 
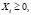
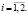
Решение задач потребительского выбора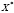 
называется точка спроса. Она зависит от цен P и дохода I и является функцией цен и дохода, т. е. функцией спроса.
Для набора из двух товаров, известных ценах на них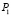 
и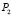 
, доходе I найти функцию спроса, если функция полезности имеет вид:
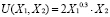
Для решения задачи используем метод множителей Лагранжа
Функция спроса имеет вид: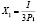 
, 
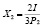
Следовательно, расход на первый товар составляет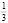 
дохода потребителя, на второй товар 
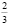дохода потребителя.
Библиографическая ссылка
Торхов А.П. МОДЕЛЬ ПОТРЕБИТЕЛЬСКОГО ВЫБОРА // Современные наукоемкие технологии. – 2013. – № 10-2. – С. 218-218;URL: https://top-technologies.ru/ru/article/view?id=33437 (дата обращения: 21.11.2024).