Задачи территориального размещения объектов возникают, например, в тех случаях, когда требуется оптимизировать сеть пунктов массового обслуживания населения. Таковыми могут быть предприятия розничной торговли, общественного питания, бытового обслуживания, почтовые отделения, станции скорой помощи, бензозаправочные стации и т.п. С одной стороны, количество пунктов должно быть минимизировано с целью сокращения расходов на их обслуживание, транспортных затрат и т.д. С другой, требуется максимально удовлетворить спрос населения на услуги пунктов сети, обеспечив доступность этих объектов. В этой ситуации можно составить задачу с двумя взаимосвязанными целевыми функциями.
Предположим, что вся территория может быть формально разделена на n районов. Пусть первоначально необходимо рационально разместить один пункт обслуживания. Имеется несколько возможных вариантов размещения пункта обслуживания: Aj,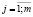 
, Количество потенциальных клиентов в каждом районе обозначим Li , 
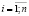. Среднее время доступа к j-й точке обслуживания от i-го района обозначим tij. В практической интерпретации задается матрица доступности районов. Тогда оптимальный вариант расположения точки обслуживания характеризуется условием минимизации общего времени, затраченного потенциальными клиентами прикрепленных районов на прибытие в пункт обслуживания Aj: 
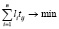. При этом производительность работы пункта Aj определяется условием 
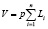, где p – норма потребления услуги на одного клиента.
Дополнительные условия модели связаны с ограничением дальности расположения пункта обслуживания. Пусть задана нормативная длительность пути к пункту обслуживания ti . Тогда вариант размещения будет считаться допустимым, если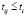 
. В противном случае вариант размещения считается недопустимым для i-го района. Этот район называется обособленным и исключается из рассмотрения. В практической реализации этот шаг реализуется через вычеркивание из матрицы доступности строк, для которых условие допустимости не выполнено. Для оставшихся районов выполняется пересчет оптимального расположения пункта обслуживания и определяется номер варианта размещения, при котором критерий минимальности суммарного времени пути будет выполнен. Производительность предприятия при этом может быть уменьшена: 
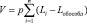. Для обособленных районов возможно, например, размещение второго предприятия.
Представленная основа модели может быть дополнена различными условиями, как например: пропускная способность пункта обслуживания, величина предприятия и т.д. Одним из возможных направлений усложнения модели также является введение дополнительных целевых функций.
Библиографическая ссылка
Севастьянова С.А., Фомина О.В. МОДЕЛЬ ТЕРРИТОРИАЛЬНОГО РАЗМЕЩЕНИЯ ПУНКТОВ ОБСЛУЖИВАНИЯ НАСЕЛЕНИЯ // Современные наукоемкие технологии. – 2013. – № 10-2. – С. 218-218;URL: https://top-technologies.ru/ru/article/view?id=33436 (дата обращения: 20.04.2024).