Согласно проведенным исследованиям различных публисцичиских источников мы установили, что коммерческая деятельность – совокупность процессов и операций, направленных на совершение купли-продажи товаров с целью удовлетворения покупательского спроса и получения прибыли.
«Коммерческая деятельность является неотъемлемой частью функционирования современных предприятий в рыночных условиях. Ключевым отличием коммерческой деятельности от прочих видов деятельности, является извлечение прибыли в процессе взаимоотношений между субъектами, которые реализуют свои действия через объекты торгового предприятия: основные производственные фонды (пассивные – здания, активные – оборудование) и товарно-материальные ценности.
С помощью математических методов в экономике и коммерческой деятельности становится возможным установление взаимосвязи между различными параметрами и факторами в производстве и реализации продукции, становится видна не только качественная, но и количественная сторона производственного цикла.
Необходимость использования математических методов диктуется тем, что последствия принимаемых решений могут касаться большого числа людей и быть связаны с огромными затратами. Поэтому степень ответственности, например, коммерсанта, значительно возрастает» [5].
«Использование математических методов в коммерческой деятельности связано со сбором необходимой информации коммерсантом, экономистом, финансистом, затем постановкой задачи вместе с математиком. Поскольку многие математические методы уже реализованы на компьютере в виде пакета стандартных программ, то доступ к ним обычно прост, автоматизирован и не составляет особых трудностей. В этом случае время решения задачи определяется в основном лишь временем ввода ее условий оператором в компьютер» [1].
Задачи коммерческой деятельности и методы их решения.
«Коммерция представляет собой сферу человеческой деятельности, включающую в себя большое количество разнообразия задач различной сложности, большинство которых сводится к решению таких задач, как распорядится имеющимися средствами (ресурсами) для достижения наибольшей выгоды или какое следует предпринять действие для получения возможно лучшего результата.
В процессе формулировки задач коммерческой деятельности следует учитывать особо форс- мажорные обстоятельства и реализм коммерческих внеплановых затрат: штрафы, обман, угрозы, воровство, грабежи, вымогательство, что негативно может отразиться на конечном результате, например, увеличением издержек при производстве продукции, что приведет к увеличению себестоимости продукции. Это может более объективно изложить содержание задачи и осуществить ее конкурентную постановку специалистами. Использование арсенала математических методов и моделей позволяет разработать оптимальные варианты решений задач коммерческой деятельности.
С точки зрения временного промежутка (горизонта планирования) можно различить задачи двух типов – задачу текущего производства (краткосрочная задача) и задачу перспективного развития (долгосрочная задача)» [3].
«Краткосрочная задача ставится на один производственный цикл – от начала производства товара до момента выхода фирмы со своим товаром на рынок. Здесь решается задача рационального использования уже имеющихся в распоряжении фирмы ресурсов, производственных мощностей, сырья, расходов на заработную плату. Поэтому математические модели краткосрочной задачи фирмы представляют собой оптимизационные задачи с ограничениями.
Долгосрочная задача охватывает период, достаточный для принятия и реализации крупномасштабных решений: наращивания или сокращения основных фондов, изменения структуры производства, определения долгосрочных инвестиций, страховок и др. Эти затраты непосредственно не зависят от объема текущего выпуска. Поэтому математические модели долгосрочной задачи фирмы являются задачами безусловной оптимизации» [2].
Математические модели и моделирование в коммерческой деятельности.
«Математическая модель – это математическое представление реальности.
Математическое моделирование – это процесс построения и изучения математических моделей.
Математические модели позволяют устанавливать взаимосвязи различных элементов экономики и коммерческой деятельности, наглядно представлять динамику развития производственного процесса» [4].
«Сущность построения математической модели состоит в том, что реальная система упрощается, схематизируется и описывается с помощью того или иного математического аппарата.
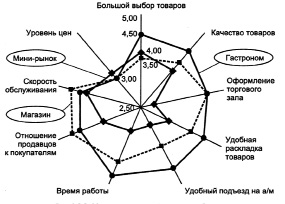
Интересной моделью является многоугольник конкурентоспособности (рисунок), показывающий соотношение различных показателей на плоскости, иногда его называют радаром или полигоном по аналогии с экраном радиолокатора. По каждой оси для отображения уровня значений каждого из исследуемых факторов используется определенный масштаб измерений, часто в виде балльных оценок. Изображая на одном рисунке многоугольники конкурентоспособности для разных предприятий, можно провести анализ уровня их конкурентоспособности по разным факторам» [2].
Библиографическая ссылка
Жидкова И.С., Латыпов Р.М., Чанышев Р.Э. КОММЕРЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ И МАТЕМАТИКА // Современные наукоемкие технологии. 2013. № 10-2. С. 208-209;URL: https://top-technologies.ru/ru/article/view?id=33428 (дата обращения: 05.03.2026).



