Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы
• Литература

Болтова Я.С. 1

---

1 Самарский государственный экономический университет

Статья в формате PDF

898 KB

1. Чернова Д.В., Сосунова Л.А. Роль логистических систем в национальной экономике // Экономические науки: научно-информационный журнал. – М.: Изд-во «Экономические науки», № 6. – 2009. 

Экономико-математическое моделирование успешно используется современными предприятиями, желающими постоянно поддерживать свою конкурентоспособность и быть востребованными на рынке. В настоящее время процесс выражения экономических явлений через математические модели интересует практически все отрасли бизнеса. При этом популярность моделирования растёт за счёт быстрого развития информационных технологий, позволяющих обрабатывать данные и строить модели разной сложности [1].

Подробнее разберём сущность моделирования, применив его к транспортному процессу. Подобная методика интересна транспортным и логистическим компаниям, так как она предоставляет возможность рассмотреть различные варианты транспортировки и выбрать оптимальный.

Для начала опишем стоящую перед нами задачу. Требуется доставить определённое количество груза из одной точки в другую таким способом, который позволит максимально сократить затраты. Актуальность исследования, связанного с нахождением наилучшего маршрута, неоспорима, поскольку с похожими задачами сталкиваются ежедневно организации и частные предприниматели.

Итак, начнём с того, что определим груз, точку отправления и точку назначения. Необходимо доставить груз из города Тель-Авив, которой находится в Израиле, до конкретной торговой точки Самары.

Чтобы показать процесс моделирования наиболее полно, в качестве груза будем рассматривать штучные единицы товара, которые в процессе исследования скомпонуем в грузовую партию. Предположим, что единица продукции имеет форму прямоугольного параллелепипеда и размер 11 см x 11 см x 8 см. Вес её составляет 350 грамм. Перевозить груз будем в стандартных коробках, размер которых составляет 0,5 м x 0,5 м x 0,5 м, а вес – 0,4 кг. В одну коробку помещается 96 единиц продукции, при этом её вес составит 34 кг. Введём ещё одно условие: необходимо перевезти 20 таких коробок. Таким образом, общий вес груза равен 680 кг, а общий объём груза – 2,5 кубических метра, при этом мы сможем перевезти 1920 единиц продукции, которые уже можно назвать грузовой партией. На этом первый этап заканчивается: грузовая партия определена.

Следующим этапом будет рассмотрение нескольких вариантов доставки груза по интересующему нас направлению. На рис. 1 представлены эти варианты.

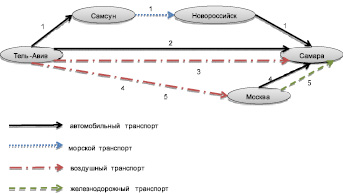
Рис. 1. Маршруты по направлению Тель-Авив – Самара

Характеристики выбранных маршрутов и организации перевозок представлены в табл, 2. В ней указаны города, где происходит смена вида транспорта (исключая города, обозначающие начальную и конечную точки), и сами виды используемого транспорта.

Таблица 1

Характеристика вариантов

Из таблицы видно, что все маршруты кроме второго включают два или три вида транспорта, то есть представляют собой мультимодальные перевозки. Для мультимодальных перевозок существенное значение приобретают таможенные процедуры, а также транспортное законодательство и коммерческие аспекты в тех странах, по которым проходит маршрут следования грузов. В нашем случае задействованы пять стран (Израиль, Сирия – город Аазаз, Грузия – город Тбилиси, Турция – город Килис и Россия), каждая из которых обязывает груз проходить таможенный контроль.

Для планирования перевозки удобно использовать сетевую модель, построение которой будет являться следующим этапом в нашем исследовании. Дуга сетевого графика представляет собой процесс непосредственной перевозки груза одним видом транспорта или выполнение какой-либо работы по погрузке, разгрузке, таможенному оформлению и так далее. Перед тем, как построить график, необходимо определить все работы, выполняемые на каждом из пяти маршрутов. Следует помнить о том, что целью построения моделей транспортировок является выбор оптимального варианта. При организации перевозки выбор варианта доставки груза производится на основе двух важнейших параметров: время и стоимость. В связи с этим помимо описания работ мы будет указывать их продолжительность и стоимость. Табл. 2 иллюстрирует порядок действий при перевозке, а также все необходимые данные для последующей оптимизации.

Таблица 2

Характеристика работ

На основании приведённых выше работ можно построить сетевую модель, описывающую транспортный процесс. При этом следует выполнять пять правил построения сетевого графика:

События должны быть правильно пронумерованы, то есть для каждой работы (i,j) i<j, где i – начало работы, а j – окончание работы.

Не должно быть «тупиковых» событий.

Не должно быть «хвостовых» событий.

Не должно быть замкнутых контуров и петель.

События должны быть связаны не более чем одной работой.

На рис. 2 представлен график, отвечающий всем требованиям и составленный по работам, описанным в табл. 2.

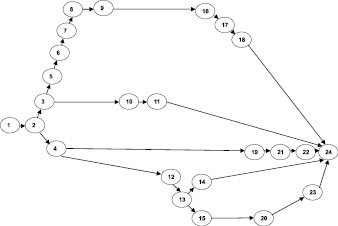
Рис. 2. Сетевая модель транспортного процесса

После упорядочивания всех работ можно переходить непосредственно к расчётам. Приведенные стоимостные и временные оценки маршрутов представляют собой два критерия, следовательно, получена многокритериальная оценка. Необходимо найти такой интегральный показатель, который будет учитывать сразу два параметра. Для получения однокритериальной оценки воспользуемся формулой, приведенной в работе Смолина Е.В. (ГУУ, Москва): С* = (Сгр +Сп)(1+Δ)n, где Сгр – закупочная стоимость товара; Сп – стоимость перевозки; (1+Δ)n – множитель наращивания процентов по процентной ставке Δ=15 % за n периодов; n = T/365; T – суммарное время маршрута. Для того чтобы применить формулу, нам нужно знать закупочную стоимость товара. Предположим, что стоимость одной единицы продукции равна 370 рублей, следовательно, общая стоимость продукции (1920 единиц) составит 710 400 рублей. Далее рассчитываем суммарную стоимость работ на каждом маршруте и суммарное время каждого маршрута, складывая соответствующие показатели конкретных работ, входящих в маршрут. Итоги вычислений представлены в табл. 3.

Таблица 3

Параметры для различных схем доставки

При формировании матрицы значения всех трёх параметров должны быть одной размерности, поэтому перед определением наилучшего результата следует перейти от абсолютных показателей, представленных в табл. 3, к относительным, рассчитанным в табл. 4. Для этого мы примем минимальное значение в каждом столбце за единицу, а остальные значения выразим в долях от единицы. Рассмотренный метод позволяет в конечном этапе получить оптимальный с точки зрения выбранного критерия способ доставки груза, по которому определяется выбор не только вида транспорта, но и схемы доставки.

Таблица 4

Относительные значения параметров

Для того чтобы исследование было завершено, нам осталось определить, какая схема доставки для нас в настоящее время оптимальная. Используем выбор варианта доставки с использованием критериев принятия решения в условиях неопределенности. Рассмотрим четыре критерия: Лапласа, Вальде, Гурвица и Сэвиджа.

Критерий Лапласа опирается на принцип недостаточного основания, согласно которому все состояния природы (в нашем случае – параметры) полагаются равновероятными. Для принятия решения для каждой схемы доставки вычисляется среднее арифметическое значение потерь. Среди средних арифметических значений по каждому маршруту выбирается минимальное, которое и будет соответствовать оптимальной схеме доставки.

Критерий Вальде рекомендует применять минимаксную стратегию, выбирая наилучшую альтернативу из наихудших. Для принятия решения для каждой схемы доставки выбирается максимальное значение параметра. После чего среди этих максимальных значений по каждому маршруту выбирается минимальное, которое и будет соответствовать оптимальной схеме доставки.

Критерий Сэвиджа состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесёт фирма, если для каждого состояния природы он не выберет наилучшей стратегии. Элемент матрицы рисков (rij) находится по формуле: rij = aij – min aij, где min aij – минимальный элемент в столбце исходной матрицы. Оптимальная схема доставки находится по формуле: min(max rij).

Критерий Гурвица придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения природы. Критерий предлагает использовать показатель степени оптимизма, который изменяется в диапазоне он нуля до единицы. На этот показатель оказывает влияние степень ответственности лица, принимающего решение по выбору схемы доставки. Чем хуже последствия ошибочных решений, тем больше желание застраховаться, а, следовательно, ближе показатель степени оптимизма к единице. Критерий Гурвица рекомендует стратегию, определяемую по формуле: min(α min aij + (1 – α)max aij), где α – степень оптимизма, а aij– элемент матрицы. Для расчётов возьмём α = 0,5.

В табл. 5 рассчитаны все четыре критерия принятия решения, на основании которых мы можем выбрать лучший маршрут.

Таблица 5

Выбор схемы доставки по критериям принятия решения

Итак, все четыре критерия указали на третий маршрут, при котором груз из Тель-Авива до Самары доставляется воздушным транспортом, и только в Самаре осуществляется перегрузка на автомобильный транспорт, который уже доставляет груз до места назначения.

Данную модель можно применять для любого вида транспорта, любого груза, любой сложности работ. Однако важно понимать, что условия на рынке постоянно меняются и эффективность различных видов доставки может варьироваться в течение всего периода выполнения договорных обязательств между грузоотправителем и перевозчиками, поэтому рассмотренные, но не реализованные варианты предпочтительно не отбрасывать, а формировать базу доставки. Возможно, что рыночная экономика будет диктовать такие условия, в рамках которых стоимость перевозки любым видом транспорта существенно изменится, а, имея в запасе дополнительные, качественно рассчитанные варианты, можно избежать кризисной ситуации.

Библиографическая ссылка