Процесс непрерывного весового дозирования сыпучих материалов широко используется в различных отраслях промышленности при реализации многих технологических процессов [1]. Основными характеристиками дозатора являются производительность и точность дозирования. Высокая точность дозирования особенно важна при производстве смесей из сыпучих компонентов, как при периодическом режиме [2, 3], так и при непрерывном [4, 5]. Кроме этого, высокая точность непрерывного дозирования необходима при организации упорядоченного смешивания сыпучих материалов [6], за счет обеспечения определенного регламента загрузки компонентов [7, 8]. Таким образом, для получения высокого качества смеси необходимо обеспечить высокую точность дозирования [9].
Процесс непрерывного весового дозирования состоит из трех основных операций: формирование непрерывного потока сыпучего материала с определенной объемной производительностью; определение весового расхода данного потока за определенный промежуток времени; расчет весовой производительности, сравнение ее значения с заданными и, при необходимости, корректировка объемной производительности.
По способу получения информации для расчета весовой производительности, весовые дозаторы непрерывного действия условно можно разделить на три большие группы [1]:
– взвешивание определенной части непрерывного потока материала, находящегося в дозаторе;
– взвешивание материала, оставшегося в бункере (технология Loss-in-weight);
– взвешивание определенной части потока на выходе из дозатора.
Первый способ, как правило, реализуется в ленточных дозаторах. Известны различные варианты установки весоизмерительного датчика, но наш взгляд, наиболее перспективной, с точки зрения повышения точности дозирования, является схема, представленная на рис. 1.
Для проведения экспериментальных исследований и сравнения результатов расчета и эксперимента, под ссыпающим краем транспортера установлены весы, цифровой выход которых соединен с управляющим контроллером. В экспериментах в качестве управляющего контроллера мы использовали персональный компьютер.
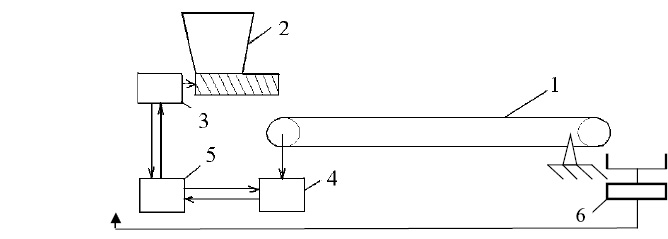
Рис. 1 Ленточный весовой дозатор:1 – ленточный транспортер; 2 – шнековый питатель; 3 – привод питателя; 4 – весовая платформа; 5 – управляющий контроллер; 6 – весы
С точки зрения расчета нагрузок на весовую платформу, ленточный транспортер представляет собой балку на двух опорах с неравномерно распределенной нагрузкой, как показано на рис. 2,а. Силовое воздействие на весовую платформу определяется из следующего условия равновесия [6]:
, (1)
. (2)
В настоящее время при расчете весовой производительности Q делается допущение о том, что сыпучий материал распределен равномерно, т.е., как это показано на рис. 2, б. В действительности, производительность шнекового питателя может иметь отклонения от заданной производительности 
. Результаты экспериментов показали, что при одних и тех же значениях реакции Aу, то есть при одних и тех же показаниях весовой платформы, массы материала, находящегося на ленте, могут быть различны, а расчетная производительность, при использовании допущения о равномерном распределении сыпучего материала на ленте, может существенно отличаться от действительной [1].
Для повышения точности непрерывного дозирования, за счет учета неравномерности распределения сыпучего материала на ленте, предлагается следующая последовательность обработки информации, поступающей в управляющий контроллер с весовой платформы. Ленту транспортера условно разделим на N участков (рис. 2). Процесс непрерывного весового дозирования будем рассматривать, как дискретный с шагом по времени 
, где L – длина транспортера, υ – скорость движения транспортерной ленты. Таким образом, непрерывный процесс будем рассматривать, как последовательность переходов (шагов) длительность каждого из которых равна Dt. На каждом переходе производительность питателя постоянна и равна q(i,j), где i – номер перехода, а j – номер участка начиная от опоры A, 
. Показания весовой платформы на i-м переходе обозначим Aу(i). В начале расчета, т.е. при i=0 будем считать, что материал распределен на ленте равномерно. В этом случае все расчетные значения qp(0, j) равны между собой и определяются по формуле:
, (3)
После первого перехода материал переместится от опоры A к опоре B на один участок, а на первый участок поступит новая порция материала q(1, 1). Расчетное значение qp(1, 1) определим по зависимости:
, (4)
На втором переходе произойдет следующее перемещение материала на один участок, а на первый участок поступит новая порция q(2,1). Расчетное значение qp(1,1) определим из уравнения равновесия системы относительно опоры B, при условии, что на втором участке вес материала равен расчетному т.е. qp(1,1), а на остальных участках qp(0, j):
, (5)
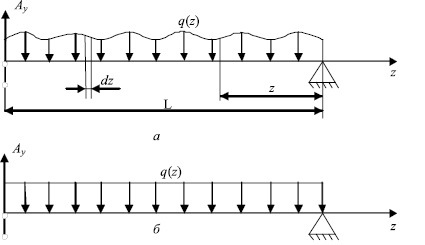
Рис. 2. Распределение сыпучего материала на ленте
На третьем переходе материал переместится еще на один участок, на первый участок поступит очередная порция материала qp(3, 1). Расчетное значение qp(3, 1) определим из уравнения равновесия системы относительно опоры B, при условии, что на третьем участке вес материала равен qp(1, 1), на втором – qp(2,1), а на остальных – qp(0, j) и так, на каждом последующем переходе.
При i=N на участке N, т.е. на ссыпающем краю транспортера будет находиться порция материала qp(1, 1). На последующих переходах, т.е. при 
можно прогнозировать производительность дозатора, определяя ее по формуле:
, (7)
где 
– промежуток времени с начала процесса до момента определения производительности, m – номер перехода.
При проведении экспериментов, материал с ленточного транспортера постоянно поступал на весы, информация с которых передавалась на персональный компьютер. Для сокращения времени на обработку результатов экспериментов, было разработано программное обеспечение (ПО), которое позволяло не только фиксировать вес материала на весах, в определенные моменты времени, но и строить зависимость изменения веса материала, т.е., так называемую, кумулятивную кривую. Выбрав интервал по времени от кумулятивной кривой легко перейти к дифференциальной кривой, которая характеризует равномерность непрерывного потока. Далее, по этой кривой в программе рассчитывается вес порции материала, который ссыпался с транспортера за выбранный интервал времени. По полученным результатам рассчитывается отклонение веса порции от заданного значения и, в конечном итоге коэффициент неоднородности.
При проведении экспериментальных исследований, а тем более при промышленном использовании описанного выше подхода, вместо весов можно использовать оптические датчики расхода [11, 12].
Таким образом, предлагаемый алгоритм расчета можно рекомендовать для получения достоверной информации о распределении сыпучего материала на ленте дозатора, погрешность не превышает погрешность весовой платформы, и использовать эту информацию при проектировании дозаторов и автоматическом управлении процессом весового непрерывного дозирования.
Библиографическая ссылка
Казаков В.А., Лазеев И.С., Пасынков В.В., Явник П.М. Имитационная модель процесса непрерывного дозирования // Современные наукоемкие технологии. – 2013. – № 8-1. – С. 86-88;URL: https://top-technologies.ru/ru/article/view?id=32494 (дата обращения: 19.04.2024).