Кафедрой Теплогазоснабжения и вентиляции БГТУ им. В.Г. Шухова разработано устройство для снижения пылеобразования при загрузке сыпучих материалов [5, 7] в аэродинамическую схему которого заложен эффект Коанда (рис. 1). Указанное физическое явление необходимо учитывать во многих технологических процессах, ему посвящались отдельные международные конференции [3], тем не менее ряд задач в литературе изучен недостаточно, хотя они имеют важное значение для практики и теории струй.
Эффект Коанда выражается отклонением по направлению к стенке (при определенных условиях прилипанием к ней) струи газа, вытекающей из сопла. Под действием вязкости на границе между струей и окружающей средой возникает слой смешения, толщина которого растет с расстоянием. Вследствие этого расход в струе также увеличивается. Таким образом, осуществляется вовлечение (эжекция) окружающего воздуха в струйное течение. Близлежащая стенка препятствует эжекции, в результате чего под струей образуется зона разрежения с давлением меньшим давления в окружающей среде. За счет поперечного перепада давления струя искривляется и устойчиво присоединяется к стенке.
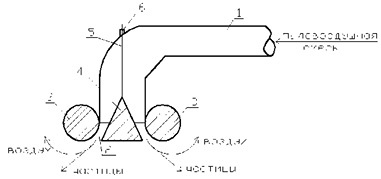
Рис. 1. Устройство для снижения пылеобразования при загрузке сыпучих материалов:1 – трубопровод пневмотранспорта; 2 – щелевое сопло; 3 – тор (разделитель потока); 4 – конус; 5 – вертикальный стержень; 6 – контргайка
Наиболее обширное применение эффект получил в пневмоавтоматике (Залманзон Л.А., Шальнев К.К, Браун Г.Л., Олсон Р.Ф.). Для модели описания эффекта в данной области техники наибольший интерес представляет лишь конечное состояние струи – отклоняется она или нет от первоначального направления. Хотя для дальнейшего исследования реализации эффекта в условиях применения разрабатываемого устройства необходимо знать не только наличие отклонения траектории, но и точку отрыва пограничного слоя нельзя пренебречь данной теорией.
Несмотря на развитие численных методов и моделей описания движения воздушных потоков, интегральные методы, используемые в пневмоавтоматике, оставались, и являются до сих пор надежным способом определения и предсказания характеристик присоединенных струйных течений в инженерном проектировании. Суть интегрального метода состоит в том, что для описания течения используются интегральные характеристики. Для струй в качестве таких характеристик выбираются потоки массы, импульса, энергии и т.д. через поперечное сечение. В рамках интегрального метода определяются именно эти характеристики, а более детальная структура течения определяется по ним с помощью априорно заданных профилей.
В работе В.Д. Столера [4] приведен краткий теоретический обзор теорий по расчету эффекта Коанда: в той или иной мере все они содержат спорные допущения и упрощения. В некоторых из них присутствует предположение о постоянстве давления в отрывной зоне, при этом вызывают вопросы баланс импульса, не учитывающий перепад давления. Профиль скорости в струе при этом принимается согласно эмпирической зависимости Шлихтинга:
, (1)
где b – характерная ширина струи.
Первое решение задачи о присоединении двумерной струи к близлежащей стенке (для частных случаев) было проведено С. Borque, B.G. Newman [1] с использованием интегрального подхода. По одному из главных предположений профиль скорости на срезе сопла является равномерным, т.е. увеличение скорости, связанное с уменьшением давления внутри отрывной зоны пренебрежимо мало. Таким образом, поток импульса на единицу длины равен
, (2)
где 
– давление окружающей среды.
Кривизна границы в направлении течения влечет за собой появление градиентов давления как вдоль по течению, так и в нормальном к стенке направлении. Однако если кривизна не очень велика, а пограничный слой очень тонок, то градиент по нормали к стенке 
обычно оказывает второстепенное влияние [2].
Роль градиента давления 
можно выявить из уравнений Прандтля для двумерного пограничного слоя:
(3)
При 
(где 
, 
) получаем:
(4)
Так что кривизна профиля скорости в окрестности стенки определяется только градиентом давления. Пусть 
(перепад давления направлен по течению – прямой перепад), тогда
при 
,
и так как профиль скорости в данном случае не имеет экстремумов, то
для всех 
,
как указано на рис. 2, а. Если течение в пограничном слое имеет место в области, где 
(обратный перепад давления), то
при 
.
Однако около внешней границы пограничного слоя и в этом случае
при 
.
Следовательно, всегда, когда 
, в профиле скорости будет появляться точка перегиба, как показано на рис. 2, б.
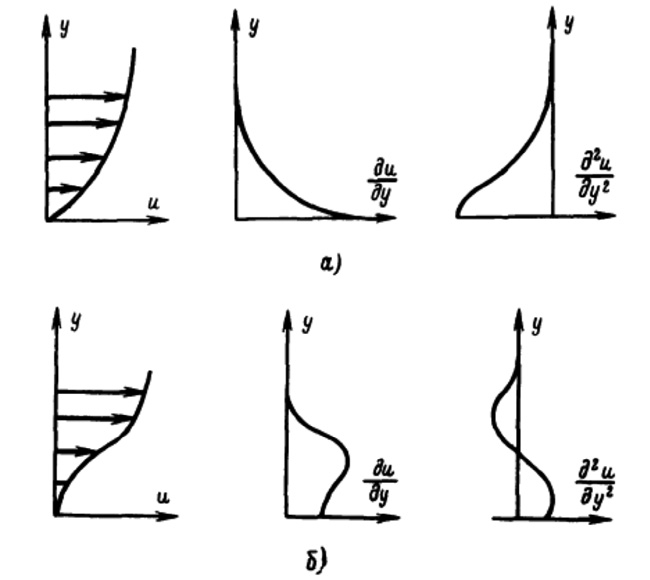
Рис. 2. Влияние градиента давления на профили скорости в пограничном слое. а – 
(
при всех y ); б – 
(
только около стенки)
При обратном перепаде давления когда 
, движение жидкости около стенки будет непрерывно замедляться, в результате чего происходит отрыв течения от поверхности (рис. 3).
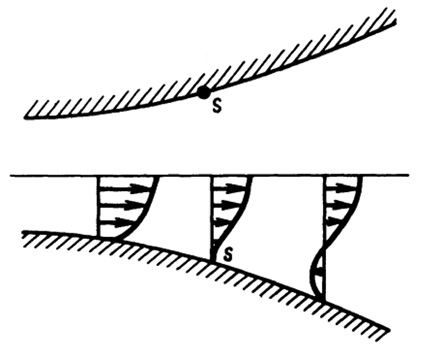
Рис. 3. Схема пограничного слоя при положительном градиенте давления:s – точка отрыва
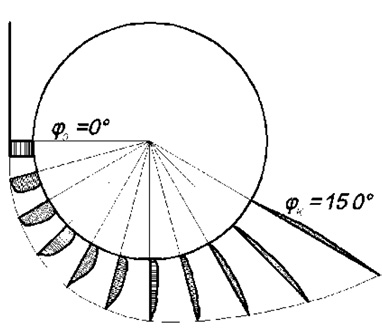
Рис. 4. Реализация эффекта Коанда при работе предлагаемого устройства
Согласно проведенным экспериментальным исследованиям [6] по реализации эффекта Коанда в условиях обтекания тороидальной поверхности сектора отрыв пограничного слоя от разделителя потока рассматриваемого устройства происходит при 
(рис. 4). Данный результат показывает актуальность и работоспособность устройства, однако следует большее внимание уделить определению градиента давления и потока импульса коандовского течения.
Несмотря на некоторые недостатки описанной интегральной модели присоединяющихся струй, они всё же компенсируются её предельной простотой. Причем во многих современных работах основные принципы остаются теми же, с внесением дополнительных уточнений и предположений.
Библиографическая ссылка
Семиненко А.С., Малахов Д.Ю., Попов Е.Н., Алифанова А.И. УЧЕТ ВЛИЯНИЯ ГРАДИЕНТА ДАВЛЕНИЯ В ИНТЕГРАЛЬНОЙ МОДЕЛИ ОПИСАНИЯ ПРИСОЕДИНЕННЫХ СТРУЙ // Современные наукоемкие технологии. – 2013. – № 8-1. – С. 52-57;URL: https://top-technologies.ru/ru/article/view?id=32426 (дата обращения: 16.04.2024).