В работе [1] автором было показано, что при условии применения в планетарном редукторе более одного сателлита, механизм теряет свою подвижность. Чтобы этого не происходило, все сателлиты кроме основного следует связывать в кинематические цепи, обладающие нулевой подвижностью, т.е. в группы Ассура.
Рассмотрим решение кинетостатики восьмизвенной группы нулевой подвижности, представленной в виде самоустанавливающейся системы четырех сателлитного планетарного редуктора (рисунок).
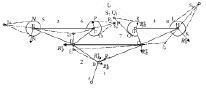
Четырехсателлитная группа нулевой подвижности планетарного зубчатого механизма
Для решения кинетостатики ко всем звеньям группы прикладываем все внешние силы и моменты сил, известным методом при заданных массах звеньев вычисляем силы и моменты сил инерции и прикладываем их в соответствующих точках звеньев. Представим решение кинетостатики группы в следующем порядке.
На продолжении линий реакций в зацеплениях звений 6, 7, 8, 9 фиксируем точки их пересечения S5, S6, S7, S8.
Из уравнений сумм моментов сил относительно обозначенных точек, определим тангенциальные составляющие реакции в опорах сателлитов (E, F, G, Н)
,
,
,
.
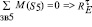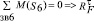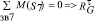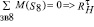1 На продолжениях линии, соединяющих точки S5-Е и S6,-F; S7-G и S8-H зафиксируем точки их пересечения – ξ3 и ξ4. Из уравнения сумм моментов всех сил, приложенных к звеньям 3 и 4
,
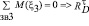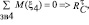
найдем тангенциальные составляющие реакции в точках D и C (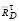
и 
).
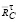Проведя затем линии, перпендикулярные к реакциям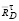 
и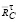 
, до их пересечения, получим точку ξ1 и из уравнения суммы моментов сил, приложенных к звену 2, относительно точки ξ2
.
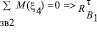Найдем первую тангенциальную составляющую реакции в шарнире В звена 2.
Обратимся далее к поводу 1 и найдем вторую тангенциальную составляющую реакцию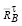 
звена 2
.
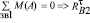Полная реакция в шарнире В, определится как векторная сумма реакций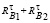 
(по закону параллелограмма)
.
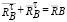При известной полной реакции в шарнире В становится возможным определить полные реакции во всех шарнирах группы и в зацеплениях колес 5,6,7 и 8
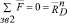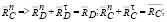
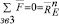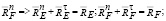
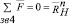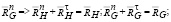
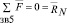и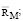 
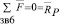и 
и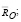 
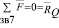и 
и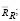 
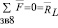и 
и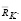 
Приведенный алгоритм силового анализа шестизвенной группы Ассура с шестью кинематическими парами четвертого класса может быть использован при силовом анализе сложных планетарных передач.
Библиографическая ссылка
Герасимов С.П. Силовое исследование сложной восьмизвенной группы Асура планетарного зубчатого механизма // Современные наукоемкие технологии. – 2013. – № 8-2. – С. 261-262;URL: https://top-technologies.ru/ru/article/view?id=32178 (дата обращения: 03.01.2025).