Повышение качества работы и надежности механизмов обуславливает ужесточение требований к качеству зубчатых передач. Точность зубчатых колес характеризуется комплексом показателей, устанавливаемых стандартами [1]. Этими показателями оперирует проектировщик, устанавливая их в качестве технических требований к изделию. Производитель же имеет дело с производственными погрешностями технологической системы, и ему бывает затруднительно связать эти погрешности с допусками, заданными проектировщиком, в частности, произвести прогнозную оценку точности изготовления. Это диктует необходимость располагать средствами учета и моделирования погрешностей технологической системы, причем во взаимосвязи с показателями качества производимого изделия.
Предлагаемый метод оценки показателей точности нарезаемых колес основан на функциональном подходе к образованию погрешностей конического зубчатого колеса, а также на применении математического аппарата преобразования координат [2]. При этом элементы технологической системы представляются как совокупность твердых тел, каждое из которых может быть заменено системой координат. Эти системы координат располагаются в той последовательности, в которой расположены элементы технологической системы в направлении от заготовки к инструменту.
Рассмотрим данный подход применительно к изготовлению конического зубчатого колеса на зуборезном станке для нарезания конических колес, схема которого представлена на рис. 1. Можно выделить следующие элементы технологической системы (рис. 1):
1. Шпиндельный узел изделия, имеет вращение, обозначаемое С’.
2. Бабка изделия, имеет перемещение по координате z’. При моделировании эта координата имеет постоянную величину.
3. Стол станка, совершает наладочное перемещение, обозначаемое В. При моделировании эта координата имеет постоянную величину.
4. Люлька, имеет вращение, обозначаемое С.
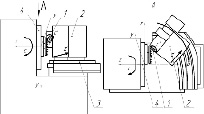
Рис. 1. Схема зуборезного станка для нарезания конических колес
Уравнение идеальной поверхности – математическое описание движения инструмента в системе координат заготовки – определяется из выражения:
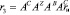 , (1),
, (1),
где rЗ – вектор, элементами которого являются координаты идеальной поверхности заготовки; AС, AZ, AB, AC, – матрицы преобразований по соответствующим координатам; rи – вектор, элементами которого являются координаты поверхности режущего инструмента.
Реальное зубчатое колесо можно рассматривать как изделие, отражающее неточности средств его изготовления, которые будут проявляться при эксплуатации, изменяясь в функции перемещения звена. Неточности средств изготовления, то есть погрешности каждого элемента технологической системы можно представить в виде малого смещения элемента как твердого тела вместе со своей координатной системой. Это малое смещение (вариация) передается через всю технологическую систему на заготовку (обрабатываемую поверхность) и моделируется матрицей вариации dAi, элементы которой представляют собой погрешности, вносимые данным элементом по соответствующей координате. Матрица вариации подставляется в выражение (1) перед матрицей соответствующего элемента.
При моделировании станка для нарезания конических колес были определены следующие функции выходной погрешности от элементов технологической системы:
– от вращения шпиндельного узла изделия:
 , (2)
, (2)
где δxsp, δysp – составляющие радиального биения шпинделя изделия, приспособления и заготовки, δzsp – составляющие осевого биения этих элементов, δAsp – составляющие торцевого биения этих элементов, dCsp – функция кинематической погрешности (неравномерности вращения) кинематической цепи изделия.
– от наладочного перемещения бабки изделия:
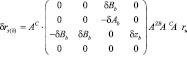 , (3)
, (3)
где δzb – погрешность позиционирования бабки изделия, dBb – отклонение от параллельности траектории перемещения относительно оси шпинделя изделия в горизонтальной плоскости; dAb – то же в вертикальной плоскости.
– от наладочного перемещения стола:
 , (4)
, (4)
где δxst – отклонение от постоянства положения оси шпинделя изделия по высоте при повороте стола; δyst – отклонение от постоянства положения оси шпинделя изделия по горизонтали при повороте стола.
– от вращения люльки:
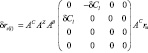 , (5)
, (5)
где dCl – функция кинематической погрешности (неравномерности вращения) кинематической цепи люльки.
Суммируя результаты выражений (2)–(5), можно определить вектор погрешностей реальной поверхности с учетом геометрических и кинематических погрешностей технологической системы. В данном случае вектор будет состоять из трех элементов по осям координат и являться функцией угла поворота люльки C, поскольку при нарезании конического колеса методом обката остальные переменные можно выразить через него:
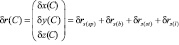 . (6)
. (6)
В элементах вектора δr(C) основное влияние имеют составляющие вида 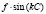 или
или 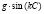 , где f, g, k – некоторые коэффициенты. Таким образом, коническое зубчатое колесо является носителем периодической ошибки, составляющие которой образуют гармонический ряд и могут быть приняты изменяющимися по синусоидальному закону. В этом ряду основная составляющая имеет наибольший период, равный одному или нескольким оборотам нарезаемого колеса, а остальные составляющие – циклические – имеют периоды меньше одного оборота колеса.
, где f, g, k – некоторые коэффициенты. Таким образом, коническое зубчатое колесо является носителем периодической ошибки, составляющие которой образуют гармонический ряд и могут быть приняты изменяющимися по синусоидальному закону. В этом ряду основная составляющая имеет наибольший период, равный одному или нескольким оборотам нарезаемого колеса, а остальные составляющие – циклические – имеют периоды меньше одного оборота колеса.
Для определения показателей точности нарезаемого зубчатого колеса необходимо проанализировать условия переноса выходной погрешности технологической системы зуборезного станка на профиль изделия. Обычно при профилировании конических колес система отсчета ошибок базируется на рассмотрении малых смещений точного плоского производящего колеса, зацепляющегося с нарезаемым колесом. Согласно классической теории точности, образование погрешности следует рассматривать по линии действия механизма. В данном случае линией действия является линия станочного зацепления n-n (рис. 2). Элементы вектора (6) приводятся к линии зацепления, т.е. проецируются на нее:
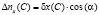 , (7)
, (7)
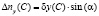 , (8)
, (8)
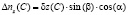 , (9)
, (9)
где β – угол наклона линии зуба; α – угол зацепления.
Просуммировав выражения (7)-(9), определяем суммарную погрешность технологической системы по линии зацепления:
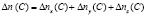 . (10)
. (10)
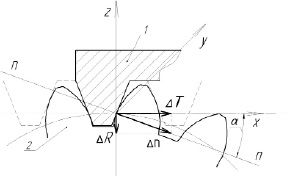
Рис. 2 Схема станочного зацепления между производящим колесом и заготовкой: 1 – резцовая головка, имитирующая зуб производящего колеса; 2 – заготовка
Полученная величина характеризует неточности положения производящего колеса относительно боковых поверхностей зубьев и может быть пересчитана в показатели точности нарезаемого колеса.
Первым этапом перехода от суммарной погрешности ∆n(C) по линии зацепления к показателям точности изготовляемого колеса является разложение ∆n(C) на радиальную ∆R(C) и тангенциальную ∆T(C) составляющие (рис. 2).
Радиальная составляющая представляется как проекция на ось Z суммарной погрешности ∆n(C) по линии зацепления:
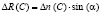 . (11)
. (11)
Тангенциальная составляющая рассматривается как проекция суммарной погрешности ∆n(C) по линии зацепленияна ось X и записывается в следующем виде:
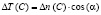 . (12)
. (12)
И тангенциальная и радиальная составляющие являются суммой множества гармоник. С другой стороны, стандартные показатели точности зубчатого колеса распределяются по нескольким группам. Из них комплекс показателей кинематической точности определяется основной гармоникой ошибок. Следовательно, для сопоставления погрешностей технологической системы стандартным показателям кинематической точности необходимо исследовать основные гармоники функций ∆R(C) и ∆T(C), то есть изменение этих составляющих за один оборот заготовки.
Радиальное биение зубчатого венца изготовленной шестерни Frr определяется по изменению радиальной составляющей ∆R(C) на промежутке от 0 до 2π, то есть как разность между максимальным и минимальным значениями функции ∆R(C) на этом промежутке.
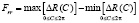 . (13)
. (13)
Аналогично, значение наибольшей кинематической погрешности 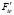 определяется как разность максимального и минимального значений тангенциальной составляющей ∆T(C) на промежутке от 0 до 2π.
определяется как разность максимального и минимального значений тангенциальной составляющей ∆T(C) на промежутке от 0 до 2π.
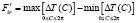 . (14)
. (14)
Комплекс показателей плавности работы определяется циклическими гармониками суммарной ошибки. Следовательно, для их определения необходимо исследовать циклические составляющие ∆R(C) и ∆T(C).
Стандартом выделяется циклический параметр – циклическая погрешность обката зубцовой частоты fcr. Определить эту величину можно, вычисляя изменение тангенциальной составляющей ∆T(C) в пределах одного углового шага, то есть при изменении С на 2π/zк, где zк – число зубьев нарезаемого колеса. В качестве итогового значения выбирается наибольшее из значений на всех промежутках:
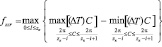 . (15)
. (15)
Предлагаемый подход позволяет установить взаимосвязь между комплексом показателей точности зубчатого колеса и производственными погрешностями. На основе этого, на стадии подготовки производства появляется возможность прогнозировать точность изготовляемых зубчатых колес. Таким образом, можно оценить возможности действующего производства по реализации возможного заказа или подобрать необходимые средства технологического оснащения для создания нового производства.
Библиографическая ссылка
Паренкина Е.В., Ахкиямов Д.Р. Моделирование точности нарезания конических зубчатых колес с круговыми зубьями методом обката // Современные наукоемкие технологии. 2013. № 8-2. С. 214-216;URL: https://top-technologies.ru/ru/article/view?id=32091 (дата обращения: 04.03.2026).



