Теория
Математический аппарат случайных марковских процессов широко используется при моделировании процессов смешивания сыпучих материалов [1, 2, 3]. Чаще всего используется одномерная цепь, а ее свойством является принадлежность частицы к конечному или бесконечно малому интервалу эйлеровой координаты. В дальнейшем будем считать этот интервал конечным и разобьем смеситель вдоль определяющей оси на m ячеек (рис. 1).

Рис.1. Графическое представление одномерной цепи Маркова
Не имея иных сведений о распределении частиц внутри ячеек, будем считать это распределение равномерным (ячейки идеального смешивания). Взятая наугад из наблюдаемой порции частица может принадлежать к одной из m ячеек, причем вероятность того, что она принадлежит к хотя бы одной из ячеек, равна единице. Вероятности принадлежности к конкретным ячейкам в общем случае различны и меняются с течением времени.
Поскольку в процессе участвует большое число частиц, то соответствующая вероятность равна доле частиц, принадлежащих ячейке, а если ячейки символизируют пространственные интервалы, то, по существу, – их относительной концентрации в ячейке. Таким образом, частица может находиться в одной из m ячеек, т. е. свойство принадлежности есть дискретная величина. Весь набор этих дискретных величин образует модельное пространство всевозможных состояний системы. Пусть начальное состояние системы характеризуется набором вероятностей Si= {S1, S2, S2, … Sm}. Очевидно, что если рассматривается эволюция фиксированной порции частиц, то
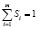 .
.
В течение промежутка времени ∆t частицы мигрируют в системе, переходя из одного состояния в другое. Будем считать, что величина ∆t достаточно мала, чтобы в течение одного перехода частицы могли переместиться только в соседние ячейки, но не далее. Эти возможные переходы показаны на рис. 1 стрелками. В результате одного перехода вектор состояния изменится и станет Sik+1. Каждый переход характеризуется своей вероятностью рij или долей частиц, перешедших из ячейки i в ячейку j за время одного перехода. Если i=j, то рjj – это вероятность частиц остаться в ячейке. Очевидно, что с ростом ∆t вероятности остаться уменьшаются, а вероятности покинуть ячейку растут. Впоследствии мы будем рассматривать процессы, когда в течение одного временного перехода возможны пространственные переходы и между удаленными друг от друга ячейками, но пока ограничимся процессом, где за малое время возможны переходы только в соседние ячейки – микромасштабное перемешивание. Если вероятности рij определены, то переход между двумя последовательными состояниями описывается системой линейных уравнений
 (1)
(1)
Система уравнений (1) может быть записана в компактной и универсальной матричной форме. Набор вероятностей, характеризующих текущее состояние системы, можно представить вектором-строкой размером 1×m:
Si= {S1, S2, S2, … Sm}. (2)
Очевидно, что в любой момент времени вектор состояния полностью характеризует весь процесс. Если цепь является цепью Маркова, то зависимость между величинами Sk и Sk+1 можно описать следующей матричной формулой:
Sk+1 = SkР (3)
 , (4)
, (4)
где Р – матрица переходных вероятностей или матрица переходов, имеющая следующий вид:
В этой матрице j-й столбец состоит из вероятностей перехода из i-го состояния. В общем случае имеются только два ограничения для вероятностей перехода pij, которые непосредственно следуют из математической постановки задачи:
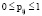 , (5)
, (5)
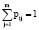 , (6)
, (6)
где i = 1,2, …, m.
Для имитации загрузки ключевого компонента в смеситель на каждом шаге или на определенных шагах периодически проводили следующую операцию:
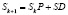 ,
,
где SD – вектор догрузки. Для того чтобы регулировать скорость перемещения ключевого компонента вдоль оси смесителя, под воздействием рабочих органов, использовали матрицу перемещений, которая имеет ту же размерность, что и матрица переходных вероятностей, но ее элементы равны либо нулю, либо единице.
Количество нулей от главной диагонали перед единицей в строке говорит о том на сколько ячеек вперед должна сдвигаться смесь конкретной ячейки за один переход. В соответствии с представленной моделью была разработана прикладная программа, описание которой дано в докладе.
Представленные в докладе результаты расчетов показывают, что при одновременном использовании двух матриц (переходных вероятностей и перемещений) возможно обеспечить достаточную независимость между диффузионной и конвективной составляющими процесса смешивания, что позволяет более адекватно учитывать влияние на интенсивность процесса смешивания физико-механических свойств смешиваемых компонентов и параметров смесителя.
Библиографическая ссылка
Земцова Е.В., Фетисов А.В., Дурнев А.С. Использование цепей Маркова для моделирования процесса смешивания // Современные наукоемкие технологии. 2013. № 8-2. С. 196-197;URL: https://top-technologies.ru/ru/article/view?id=32076 (дата обращения: 23.02.2026).



