Одной из составных частей дорожной одежды является верхний ее слой, называемый дорожным покрытием.
Покрытие высокого класса производится из асфальтобетонной смеси, содержащей повышенное количество мелкого щебня (50-75 %), повышенное количество битума до (6-8 %) с ведением целлюлозы, минерального порошка (8-12 %).
Асфальтобетон может быть различного типа [1] в зависимости от требований к строящемуся объекту. Рассмотрим щебеночно-мастичный асфальтобетон как наиболее распространенный вид покрытия, применяемый практически на всей территории России несмотря на многообразие климатических зон. Механические характеристики такого материала в среднем составляют: модули упругости для битума – 550 МПа, для щебня – 7000 МПа. Процесс укладки первого слоя можно описать следующим образом: щебень мелкозернистой фракции насыпается на подготовленную насыпь из более крупной фракции и укатывается. Затем битумно-распределительная машина заливает его разогретым битумом, поверх насыпают мелкий щебень и укатывают его по горизонтали. Затем укладывают второй слой, третий – всего от 2 до 5 слоев. Толщина каждого слоя 5-7,5 см, температура вяжущей смеси 175 °С. За счет добавки специальных вяжущих средств (WAM – пена, Асфамин и т.д.) происходит расширение связующего вещества и образование пенистых структур в асфальтобетоне. Это дает возможность использовать прокладку дорожных покрытий при более низких температурах.
Из описания технологии асфальтобетона следует, что это композитный материал. Основные признаки композита: составная структура, наличие связующего и наполнителя. Ввиду неупорядоченного расположения структурных элементов в связующем можно утверждать, что расположение включений в структуре случайно. Для изучения механических свойств компонентов асфальтобетона в процессе эксплуатации необходимо построить модель структуры [2]. Принципы построения моделей в механике сплошной среды известны из литературы [3]. Следует отметить, что всякая модель должна удовлетворять принципам, необходимым для оценки качества различных конкретных моделей: адекватность оригиналу, обсчитываемость, соответствие.
Модель тем более адекватна оригиналу, чем большим количеством свойств оригинала она наделена. Но степень близости к оригиналу не может быть бесконечна: всякая полезная модель должна быть обсчитываема. Это значит, что должен существовать математический аппарат, с помощью которого можно описать свойства данной модели. Степень установления построенной модели уже имеющимся классическим моделям дает принцип соответствия.
Особенностями модулируемой среды являются: неоднородность, случайность расположения включений, наличие резко выраженной границы между компонентами. Будем считать включения сферическими элементами с разбросом радиусов в определенных небольших пределах, компоненты среды деформируются упруго вплоть до разрушения. Таким образом будем строить модель упругой сплошной кусочно-однополюсной среды со случайным расположением круговых включений в плоскости. Кроме того, будем считать, что размеры включений (зерен щебня) малы в сравнении с размерами всего изделия (полотна дорожного покрытия), число включений велико и расположение их не упорядоченно (случайно).
Сформулирована задача статистической механики композитных материалов о построении статистической модели среды асфальтобетона. Заданными параметрами считаем массив случайных размеров включений, процент содержания включений, размеры построенного поля.
На языке Delphi решена задача моделирования стохастической структуры.
Основные этапы программирования:
1) основные ограничения:
расстояния между центрами окружностей:
;
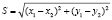критерии пересечения окружностей:
.
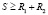2) процесс заполнения:
размер области, площадь области.
3) Используемые подпрограммы:
Random(Р) – функция, задающая нормальное распределение в интервале (0 – Р) некоторой случайной величины.
4) ограничения зоны попадания окружностей:
.
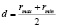5) Процесс бросания окружностей в заданную область:
,
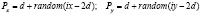где Рх, Ру – координаты центра окружности.
6) Определение минимально возможного радиуса окружности для данной точки в пределах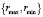 
. Обозначим его minxy, для этого вычислим:
7) Процесс выборы радиуса:
.
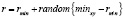8) Проверка условия:
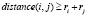– пересечение построенного круга с уже имеющимися.
Если случайно построенный круг не пересекается со всеми уже имеющимися, то добавляем его в массив и увеличиваем число включений qr на единицу.
9) Проверка условия коэффициента заполнения (процентного содержания включений)
,
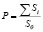где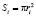 
, S0 – общая площадь поля.
Если число Р удовлетворит условию, то программа заканчивает работу. Если условие заполнения области не выполнено, то переходим к построению следующего круга.
Составлена программа для графического вывода полученной области на экран. Ограничения в работе: при Р > 0,5 процесс заполнения занимает много вычислительных ресурсов и времени.
На этот случай вводится ограничение на количество окружностей.
Библиографическая ссылка
Дроздов П.А., Бойко Л.А., Штагер Е.В. ПОСТРОЕНИЕ СТАТИСТИЧЕСКОЙ МОДЕЛИ СТРУКТУРЫ АСФАЛЬТОБЕТОННОГО ДОРОЖНОГО ПОКРЫТИЯ // Современные наукоемкие технологии. – 2013. – № 8-2. – С. 193-194;URL: https://top-technologies.ru/ru/article/view?id=32073 (дата обращения: 03.01.2025).