Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы
• Ключевые слова
• Литература

Савицкий И.В. 1 Матвеева Т.А. 1

---

1 Волжский политехнический институт, филиал Волгоградского государственного технического университета

Статья в формате PDF

727 KB

1. Кочин Н.Е. Введение в векторный и тензорный анализ.

2. Клетеник Д.В. Сборник задач по аналитической геометрии.

3. Высшая математика для технических университетов. Линейная алгебра: учебное пособие / В.Н. Задорожный, В.Ф. Зальмеж, А.Ю. Трифонов, А.В. Шаповалов.

В разделе математики «Линейная алгебра и аналитическая геометрия» мы изучили скалярное, векторное и смешанное произведения векторов. Я случайно увидел в некоторых книгах информацию о двойном векторном произведении и решил подробнее узнать о нём и его свойствах.

Пусть вектор умножается векторно на вектор , после чего полученный вектор 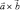умножается снова векторно на вектор . В результате получается так называемое двойное векторное произведение 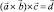(ясно, что в результате имеем 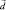-вектор).

Двойное векторное произведение вычисляется по формуле

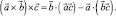(1)

В общем случае, 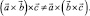Покажем это, используя свойства векторного и скалярного произведения двух векторов

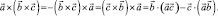(2)

Из сопоставления формул (1) и (2) можно вывести следующее правило для запоминания: двойное векторное произведение равно произведению среднего вектора на скалярное произведение двух других, минус крайний вектор скобки, умноженный на скалярное произведение двух других или говорят 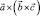равно «б а ц» минус «ц а б».

При круговой перестановке векторов 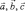формула (1) приводит к трем разным векторам:

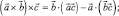
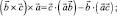
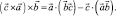
Складывая вместе эти три равенства, получим тождество

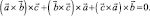
Одно из применений формулы (2) состоит в выводе разложения данного вектора , на две компоненты, из которых одна параллельна, а другая перпендикулярна к заданному вектору . В самом деле, положив в формуле (2) 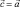, найдем:

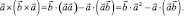
Решая это уравнение относительно , получим:

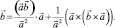(3)

Первый из слагаемых векторов правой части, очевидно, параллелен вектору , а второй перпендикулярен к нему. Формула (3) для разложения упрощается, если есть единичный вектор. Тогда и формула (3) примет вид:

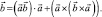
Рассмотрим следующий пример: показать, что если 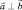то

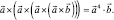
По формуле (2) имеем

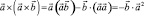
т.к. .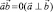

Умножая векторно слева на , получим:

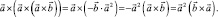
Повторяя ту же операцию, найдем:

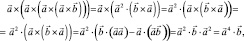
что и требовалось.

Таким образом, я познакомился с двумя случаями произведений трех векторов в трехмерном пространстве: скалярно-векторное (в результате получаем число) и двойное векторное произведение (в результате получаем вектор).

Библиографическая ссылка