Потребительский спрос на некоторый товар зависит от большого числа факторов: цены товара, цен на другие товары, сезонности, дохода покупателя и т.д. Если же все факторы, кроме цены p, неизменны, то зависимость спроса D от цены можно рассматривать как функцию D = D(p). Аналогично можно рассмотреть функцию предложения S = S(p) – зависимость количества товара S, предлагаемого к продаже производителями, от цены товара p, которая сложилась на рынке. Равновесная цена p0 при этом определяется как равенство спроса и предложения: S(p0) = D(p0).
Равновесие спроса и предложения изменится при введении акциза по ставке t ∈ (0; 1), тогда новой станет цена, удовлетворяющая условию: S((1 – t)pt = D(pt).
При цене товара p его стоимость для потребителя равна p, а выручка производителя от продажи единицы продукции равна (1 – t)∙p. При этом может показаться, что бремя акцизов ложится целиком на потребителя, т.е. при введении акциза по ставке t цены возрастают в 1/(1 – t) раз, так чтобы после взимания налогов производитель получил туже выручку от продажи единицы товара, что и раньше: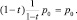 
Рассмотрим пример, который позволит убедиться в неверности такого предположения.
Пример. Пусть на рынке некоторого товара известны функции предложения S(p) = 2p – 2 и спроса D(p) = 10 – p. Требуется определить, как изменится равновесная цена товара, реализованный спрос и выручка производителя при введении акциза по ставке t ∈ (0; 1)? Проанализировать полученные результаты при установлении ставки акциза на уровне 1, 5, 20, 50 и 90 %.
Решение. Найдём равновесную цену до введения акциза:
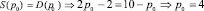(ден. ед.).
Определяем равновесную цену после введения налога:
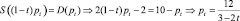(ден. ед.).
Заметим, что pt > p0 для t ∈ (0; 1), при этом:
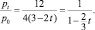
Полученное соотношение показывает, что на потребителя ложится бремя оплаты двух третей введённого налога, а оставшуюся треть платит производитель.
Чтобы выяснить, на сколько процентов вырастает цена при введении акциза, преобразуем последнее выражение:
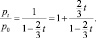
Отсюда следует, что введение акциза при ставке t = 1, 5, 20, 50 и 90 % приводит к увеличению цены (таблица).
Естественно, что увеличение цены приводит к уменьшению объёма реализованного спроса и предложения, а значит, к уменьшению выручки производителя. До введения налога в точке равновесия реализовывался спрос D(p0) = 10 – p0 = 6 (ед.), с введением акциза спрос стал равен
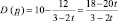(ед.).
Найдём отношение нового и старого значений спроса:
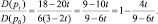
При ставке акциза t = 1, 5, 20, 50 и 90 % из последнего выражения следует, что спрос снижается (таблица).
Теперь исследуем, как изменится выручка производителя при введении акциза. До введения акциза выручка равна p0∙D(p0) = 4∙6 = 24 (ден. ед.), после введения (с учётом уплаты налога) – выручка изменяется до
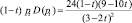(ден. ед.).
При этом
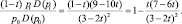
При ставке акциза t = 1, 5, 20, 50 и 90 % следует, что выручка уменьшается (таблица).
|
Ставка, t (%) |
1 |
5 |
20 |
50 |
90 |
|
Увеличение цены, (%) |
0,07 |
3,4 |
15,4 |
50 |
150 |
|
Уменьшение спроса, (%) |
0,8 |
4 |
17,1 |
50 |
100 |
|
Уменьшение выручки, (%) |
0,4 |
2,3 |
10,3 |
33,3 |
100 |
Таким образом, увеличение ставки акциза приводит к увеличению цены на товар, но при этом происходит снижение спроса и выручки. Причём при ставке t = 90 % спрос и выручка падают до нуля (происходит уменьшение на 100 %).
Найдём такую ставку акциза, которая обеспечит максимум налоговых поступлений. Для определения максимальной ставки акциза, решим задачу:
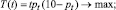
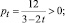0 < t < 1,
или
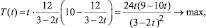
0 < t < 1.
Находим производную: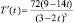 
и определяем критические точки: 9/14 и 3/2, отсюда 
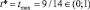. При ставке акциза 
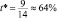оказывается, что равновесная цена
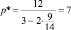(ден. ед.)
на 75 % выше, чем на рынке без акциза; равновесный спрос составляет D(p*) = 10 – 7 = 3 (ед.) – это в два раза меньше, чем на рынке без акциза. При этом налоговые поступления составляют
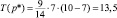(ден. ед.),
а выручка
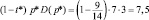(ден. ед.),
что на 69 % меньше, чем до введения акциза.
Таким образом, между акцизом и налогом на прибыль есть существенные различия. В отличие от налога на прибыль, который является только инструментом перераспределения части доходов от успешных производителей в пользу государства, акциз является также инструментом рыночного регулирования, позволяя не только перераспределять доходы, но и регулировать объёмы производства товаров.
Библиографическая ссылка
Рассоха Д.С., Гарина М.С., Алексеева И.Ю., Агишева Д.К., Светличная В.Б. МАТЕМАТИЧЕСКИЙ АНАЛИЗ МОДЕЛИ НАЛОГООБЛОЖЕНИЯ // Современные наукоемкие технологии. – 2013. – № 6. – С. 107-108;URL: https://top-technologies.ru/ru/article/view?id=32011 (дата обращения: 21.11.2024).