По трубопроводу диаметром 25×2,5 самотеком стекает нитробензол с температурой 20 °С. Начальная точка трубопровода выше конечной на 200 мм. Длина горизонтальной части трубопровода 240 м. Определить массовый расход нитробензола.
Имеем исходные данные: диаметр трубопровода: dн = 252,5 мм (диаметр наружный×толщину стен); длина трубопровода: l = 240 м; жидкость: нитробензол t = 20 °С.; разность между начальной и конечной точками трубопровода h = 200 мм. Необходимо определить массовый расход нитробензола G [кг/с].
При самотечном движении нитробензола по прямой круглой трубе в отсутствии местных сопротивлений потери энергии зависят от длины трубопровода и обусловлены силами вязкости и влиянием твердых стенок, ограничивающих поток. Разность высот концов трубопровода составляет 200 мм, что мало по сравнению с длиной, которая равна 240 м. Следовательно, можно предположить, что режим движения жидкости – ламинарный, то есть Re1 ≤ 2300.
Пусть Re1 = 500. Определяем скорость движения нитробензола из критерия Рейнольдса:
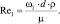
Имеем
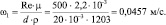
Вычислим потери на трение по формуле Дарси–Вейсбаха:
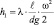[м],
где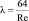 
для ламинарного движения. Подставляем данные, получаем:
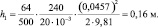
Заметим, что разность высот концов трубопровода должна быть равна h = 200 мм = 0,2 м. Таким образом, число Рейнольдса, выбрано неверно, так как необходимо выполнение равенства: h1 = h.
Пусть Re2 = 1000. Определяем скорость движения нитробензола:
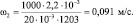
Вычислим потери на трение:
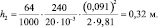
И в этом случае, получаем, число Рейнольдса, выбрано неверно, так как мы получили h2 > h, а должно быть h2 = h.
Приведенные расчеты позволяют построить график зависимости величины h от числа Re: при Re1 = 500 h1 = 0,16 м; при Re2 = 1000 h2 = 0,32 м
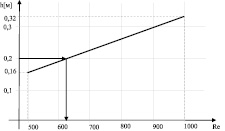
Графическое решение
Полученный графически результат числа Рейнольдса подставляем в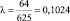 
и вычисляем скорость движения нитробензола:
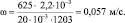
Таким образом, имеем потери в трубопроводе:
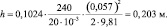
Полученное значение числа потерь практически равно заданному по условию h = 200 мм = 0,2 м.
Таким образом, зная скорость движения нитробензола в трубопроводе, получаем массовый расход нитробензола:
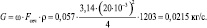
Библиографическая ссылка
Перепеченова Т.Н., Мокрецова И.С., Ребро И.В., Мустафина Д.А. Геометрический метод математического расчета массового расхода нитробензола // Современные наукоемкие технологии. – 2013. – № 6. – С. 106-107;URL: https://top-technologies.ru/ru/article/view?id=32010 (дата обращения: 21.11.2024).