Рассмотрим двухфакторную производственную функцию Y = F(K, L), где K и L – затраты капитала и труда соответственно, при этом Y – объём выпуска (в денежном выражении). Пусть цены факторов производства составляют соответственно PK и PL. Тогда прибыль производителя будет равна
Π(K, L) = F(K, L) – PK⋅K – PL⋅L. (1)
Цена труда – это заработная плата работника. Цена капитала равна денежной сумме, которая в единицу времени тратится на содержание единицы капитала, таким образом, цена капитала равна норме амортизации – величине амортизационных отчислений на 1 ден. ед. производственных фондов.
Будем считать основной целью производителя – стремление получить максимальную прибыль, тогда математическая формулировка задачи производителя имеет вид: требуется определить такую организацию производства (т.е. такие объёмы затрат ресурсов), которые приносят наибольшую прибыль.
Π(K, L) → max; K ≥ 0, L ≥ 0. (2)
В задачу (2) подставим выражение (1):
Π(K, L) = F(K, L) – PK⋅K – PL⋅L → max;
K ≥ 0, L ≥ 0. (3)
Для решения задачи максимизации необходимо найти частные производные прибыли по капиталу и труду и приравнять их к нулю:
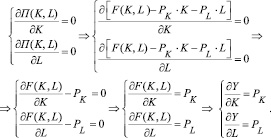(4)
Любая точка (K*, L*), удовлетворяющая условиям (4), будет точкой максимума прибыли, и при этом оптимальные затраты ресурсов K* и L* будут неотрицательными, следовательно, условия (4) определяют оптимальное решение задачи производителя.
Рассмотрим экономическую интерпретацию условий максимума прибыли производителя. В левых частях этих условий находятся предельные эффективности ресурсов, а в правых – цены ресурсов, поэтому условия (4) можно интерпретировать следующим образом: производитель достигает максимальной прибыли при таких затратах ресурсов K* и L*, что предельные эффективности ресурсов равны их ценам.
Пример. О фирме с мультипликативной производственной функцией, имеющей вид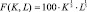 
, известны факты: производственные фонды K = 100 000 000 ден. ед., всего в фирме занято L = 1000 сотрудников. Средняя заработная плата W = 1000 ден. ед в месяц и период амортизации основных производственных фондов n= 12 месяцев. Требуется рассчитать оптимальный размер и оптимальную численность работников. Определить, во сколько раз увеличится прибыль фирмы при переходе к оптимальным затратам факторов производства.
Решение. Цена труда PL = W = 1000 – это заработная плата, а цена капитала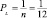 
ден. ед. равна ежемесячным амортизационным отчислениям на содержание одной денежной единицы производственных фондов, поэтому прибыль фирмы при таких затратах труда и капитала равна по формуле (1):
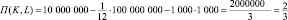млн. ден. ед.
Оптимальные параметры фирмы задаются условиями (4), состоящими в том, что предельные эффективности ресурсов должны быть в оптимальной точке равны ценам ресурсов. В этом случае предельная фондоотдача и предельная производительность труда равна соответственно
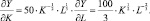
Поэтому оптимальные условия фирмы (4) принимают вид:
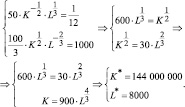
При этом выпуск фирмы составит
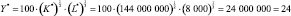млн. ден. ед.,
а прибыль
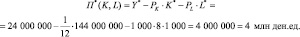
Полученный результат показывает, что оптимальный выбор затрат капитала и труда позволил увеличил прибыль в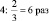 
раз.
Библиографическая ссылка
Глотова А.В., Лосева А.Ю., Ульянова А.В., Агишева Д.К., Зотова С.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПОВЕДЕНИЯ ПРОИЗВОДИТЕЛЯ // Современные наукоемкие технологии. – 2013. – № 6. – С. 95-96;URL: https://top-technologies.ru/ru/article/view?id=32001 (дата обращения: 21.11.2024).