В современной экономике используется множество математических методов, разработанных ещё в 20 веке. Применение линейной алгебры значительно упростило решение многих экономических задач. В данной работе рассматриваются основные способы решения задач с помощью элементов линейной алгебры.
Понятие матрицы и основанный на нем раздел математики – матричная алгебра – имеют большое значение для экономистов, основная часть математических моделей экономических объектов и процессов записывается в простой и компактной матричной форме. С помощью матриц удобно описывать различные экономические закономерности. Например, дана следующая таблица средних розничных цен на автомобили в зависимости от срока их службы (условных единиц).
|
Продолжительность службы (годы) |
Годы |
||
|
2005 |
2006 |
2007 |
|
|
1 |
1881 |
2120 |
2445 |
|
2 |
1512 |
1676 |
1825 |
|
3 |
1261 |
1397 |
1484 |
|
4 |
1054 |
1144 |
1218 |
Предложенную таблицу можно записать в виде матрицы следующим образом:
где содержательное значение каждого показателя определяется его местом в матрице. К примеру, число 1825 во второй строке третьего столбца представляет собой цену прослужившего 2 года автомобиля в 2007 году. Аналогичным образом находим, что числа, записанные в строку, характеризуют цены автомобилей, прослуживших один и тот же срок в различные годы, а числа в столбце – цены автомобилей различного срока службы в данном году.
Таким образом, место, занимаемое числом в матрице, характеризует продолжительность использования автомобиля и год, к которому относится цена.
Применение матриц при решении экономических задач рассмотрим на следующем примере. Предприятие выпускает продукцию трех видов P1, P2, P3 и использует сырье двух типов: S1, S2. Нормы расхода сырья характеризуются матрицей:
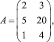
где каждый элемент aij (i = 1, 2, 3; j = 1,2) показывает, сколько единиц сырья j-го типа расходуется на производство единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой C = (100 80 130).Стоимость единицы каждого типа сырья (денежных единиц) – матрицей-столбцом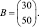 
. Необходимо найти общую стоимость сырья.
Решение: Затраты первого сырья составляют S1 = 2∙100 + 5∙80 + 1∙130 = 730единиц, а второго S2 = 3∙100 + 2∙80 + 4∙130 = 980 единиц. Значит затраты сырья S могут быть записаны в виде матрицы строки (730 980) и произведения:
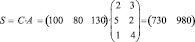
Общая стоимость сырья
Q = 730∙30 + 980∙50 = 70900 (денежных единиц)
может быть записана в следующем виде:
Q = S∙B = (CA)B = (70900).
Вывод: общая стоимость сырья составляет 70900.
Также экономические задачи можно решать с помощью систем линейных уравнений.
Рассмотрим и решим с помощью системы линейных уравнений следующую задачу:
Из определенного листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице:
|
Тип заготовки |
Способ раскроя |
||
|
1 |
2 |
3 |
|
|
А |
3 |
2 |
1 |
|
Б |
1 |
6 |
2 |
|
В |
4 |
1 |
5 |
Записать в математической форме условия выполнения задания.
Решение: Обозначим через x, y, z количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. Тогда при первом способе раскроя x листов будет получено 3 заготовок типа А, при втором – 2y, при третьем – z. Для полного выполнения задания по заготовкам типа А должно выполняться равенство:
.
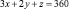Таким же способом получаем уравнения:
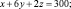
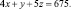
Имеем систему:
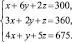
Данным уравнениям должны удовлетворять неизвестные x, y, z для того, чтобы выполнить задание по заготовкам Б и В. Полученная система линейных уравнений и выражает в математической форме условия выполнения всего задания по заготовкам А, Б и В.
Решим систему методом Гаусса.
1. Запишем систему в виде матрицы.
2. Составим расширенную матрицу системы.
3. Приведём полученную матрицу к треугольному виду.
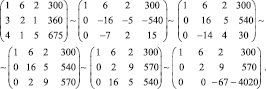
Исходная система равносильна следующей:
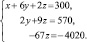
Решая полученную систему, имеем: x = 90, y = 15, z = 60.
Вывод: вектор C (90, 15, 60) есть решение системы.
Также, говоря, о роли линейной алгебры в экономике нельзя не упомянуть о модели многоотраслевой экономики Леонтьева, которая была разработана в виде математической модели в 1936 году. Эта модель основана на алгебре матриц и использует аппарат матричного анализа.
Рассмотрим задачу:
В таблице приведены коэффициенты прямых затрат и конечная продукция отраслей на плановый период, усл. ден. ед.
|
Отрасль |
Потребление |
Конечный продукт |
||
|
Промышленность |
Сельское хозяйство |
|||
|
Производство |
Промышленность |
0,3 |
0,2 |
300 |
|
Сельское хозяйство |
0,15 |
0,1 |
100 |
|
Найти: плановые объёмы валовой продукции отраслей, межотраслевые поставки, чистую продукцию отраслей.
Решение:
1. Выпишем матрицу коэффициентов прямых затрат A, вектор конечной продукции Y:
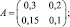
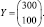
Заметим, что матрица A продуктивна, так как её элементы положительны и сумма элементов в каждом столбце меньше единицы.
2. Найдем матрицу
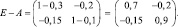
Тогда матрица полных затрат:
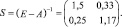
3. По формуле X = (E – A)–1⋅Y = SY найдем вектор валового продукта X:
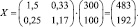
4. Межотраслевые поставки xij найдём по формуле xij = aij∙xj
X11 = a11∙x1 = 0,3·483 = 144,9;
X12 = 0,2·192 = 38,4;
X21 = 0,15·483 = 72,45;
X22 = 0,1·192 = 19,2.
5. Чистая продукция промышленности равна: 483 – 144,9 – 72,45 = 265,65
Чистая продукция сельского хозяйства: 192 – 38,4 – 19,2 = 134,4.
Итак, рассмотрев в данной статье некоторые задачи и их решения, можно сказать, что это лишь небольшая часть математических методов, используемых в экономике. Экономика и математика, очень тесно связаны и постепенно математические методы и модели начинают занимать очень важное место в экономике.
Библиографическая ссылка
Цысь Ю.В., Долгополова А.Ф. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И ИХ ПРИМЕНЕНИЕ ПРИ РЕШЕНИИ ЭКОНОМИЧЕСКИХ ЗАДАЧ // Современные наукоемкие технологии. – 2013. – № 6. – С. 91-93;URL: https://top-technologies.ru/ru/article/view?id=31998 (дата обращения: 21.11.2024).