Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы
• Ключевые слова
• Литература

Невидомская И.А. 1 Якубова А.М. 1

---

1 Ставропольский государственный аграрный университет

Статья в формате PDF

441 KB

1. Грень Е. Статистические игры и их применение. – М.: Статистика. – 2005. – 176 с.

2. Кобринский Н.Е., Кузьмин В.И. Точность экономико-статистических моделей. – М.: Финансы и статистика – 2001. – 255 с.

3. Математико-статистические методы в экономическом анализе и планировании / отв.ред. Б.Б. Розин Из-во «Наука», Сибирское отделение. –Новосибирск, 1983. – 254 с.

4. Невидомская И.А. Применение методов оптимизации для решения экономических задач // сб. науч. статей по материалам III Всероссийской конференции. – Ставрополь, 2010. – С. 163-165.

5. Невидомская И.А. Математическое моделирование экономических ситуаций на основе выбора оптимальной стратегии по управлению бизнесом // Сб. науч. статей по материалам III Всероссийской конференции. – Ставрополь, 2010. – С. 165–169.

При анализе экономических явлений и процессов мы сталкиваемся с многомерностью их описания, то есть с необходимостью учитывать большое число признаков. При этом, не всегда представляется возможным сразу выделить наиболее существенные, главными из них. Поэтому естественной попыткой является возможность сконцентрировать информацию, выразить большое число исходных косвенных признаков одним или несколькими наиболее емкими, информативными признаками. Назовем их основными признаками.

Основные признаки конструируют по определенным алгоритмам на основе исходных, единичных признаков. Основные признаки должны быть наиболее существенными, определяющими. Именно для такого интегрирования информации и используется факторный анализ. Сущность его заключается в описании и затем в переходе от описания объекта большим количеством единичных, непосредственно измеряемых признаков к описанию их меньшим числом сконструированных интегральных переменных, отражающих наиболее существенные черты исследуемого объекта.

Под факторами будем понимать основные признаки, являющимися некоторыми функциями единичных исходных признаков.

Концепция факторного анализа сводится к следующим положениям:

– все исходные признаки необходимо пронормировать, то есть осуществить переход от параметра к нормированному

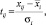(1)

где xij – значение i-го признака для j-го объекта; – среднее значение и среднее квадратическое отклонение для i-го признака.

При этом дисперсии пронормированных переменных равны. Единичные дисперсии каждой переменной включают в себя общность и характерность. Общность – часть дисперсии i-й переменной, которая обусловлена общими для двух или переменных факторов.

Под характерностью будем понимать часть дисперсии i-й переменной, которая связана с фактором, присущим только i-й переменной и случайной ошибкой. На составные части характерность раскладывается сравнительно редко.

Общность есть коэффициент множественной детерминации i-го признака со всеми общими факторами. Общность может быть разложена по каждому из k факторов, то есть 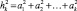. Величины 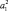,,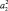 …, будем называть факторными нагрузками. Необходимо отметить, что между общими факторами связь отсутствует.

Основная часть характеристики, которой является специфичность 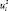, вместе с общностью 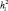образуют надежность

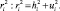(2)

Данные характеристики определяются на основе матрицы коэффициентов корреляции между исходными признаками.

Рассмотрим принципиальные подходы к решению каждой из обозначенных проблем.

Проблема общности. Для определения общности используется довольно много процедур. Почти все они базируются на той предпосылке, что общность i-го признака должно быть заключена в пределах

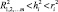(3)

где 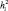– общность для i-го признака; 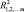– коэффициент множественной детерминации i-го признака со всеми остальными признаками; 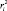– надежность.

Наиболее часто при оценке общности применяют способ наибольшей корреляции, когда в качестве оценки общности берется наибольший коэффициент корреляции i – го признака со всеми другими признаками. Теоретически этот метод не обоснован и дает предварительную, грубую оценку. Общность может быть определена расчетным методом, в основе которого лежит предварительный расчет факторов методом главных компонент.

После выбора по определенному критерию главных факторов находим факторные нагрузки, а на их основе – общность

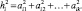(4)

Таким образом, проблема факторов состоит в определении числа факторов и нагрузок каждого из них по исходным переменным. Для решения проблемы факторов применяются различные методы. Однако в настоящее время наиболее часто применяют метод главных факторов или центроидный метод. Под методом главных факторов подразумевается приложение метода главных компонент к редуцированной матрице парных коэффициентов корреляции между исходными признаками. На диагонали этой матрицы вместо единиц стоят общности.

Найти фактор означает определить вектор его нагрузок на исследуемые признаки. Алгебраически определение векторов нагрузок факторов основывается на предпосылке, что первый из выделенных факторов описывает максимум дисперсии всех признаков, второй – максимум оставшейся дисперсии и т.д. Для реализации этой предпосылки необходимо построить систему однородных уравнений, необходимым и достаточным условием которой будет являться равенство нулю детерминанта матрицы коэффициентов этих уравнений.

Проблема нахождения корней и соответствующих им векторов решения в математике имеет название проблемы собственных значений и собственных векторов для матрицы.

Составной частью проблемы факторов является определение их числа. В практике чаще всего используются три метода нахождения числа выделяемых факторов:

– процедура выделения факторов заканчивается, если выделено 90-95 % полной дисперсии признаков;

– процедура выделения факторов заканчивается, когда следующий фактор объясняет менее 3-5 % полной дисперсии признаков;

– проверяется гипотеза о том, что выделенных общих факторов вполне достаточно для воспроизведения корреляционной матрицы.

Проблема вращения факторов. Цель факторного анализа состоит в том, чтобы на основе большого числа исходных переменных сконструировать гипотетические переменные (факторы), их объясняющие. Выделенные факторы должны отражать содержание исходных данных. Однако, факторы, выделенные методом главных факторов или другим методом, редко содержательно интерпретируются. Их нагрузки очень чувствительны к введению новых переменных. Цель вращения – найти такие факторы, которые легко интерпретировать по исходным данным. При этом появление новых признаков не должно оказывать сильного влияния на величину факторных нагрузок. Критерием вращения служит так называемая простая структура. К простой структуре предъявляются следующие требования:

– каждый признак должен иметь высокие факторные нагрузки хотя бы с одним фактором;

– каждый признак должен иметь высокие факторные нагрузки не менее чем с r переменными;

– должны иметь место такие признаки, которые с одним фактором имеют нулевую или близкую к ней нагрузку, а с другими максимально большую;

– если число факторов больше четырех, то необходимо иметь как можно больше переменных с нулевыми нагрузками;

– следует стремиться к тому, чтобы иметь как можно меньше переменных с высокими факторными нагрузками по двум и более факторам.

Алгебраически процесс вращения можно записать следующим образом:

A* = A⋅T, (5)

где A* – матрица факторных нагрузок после вращения; A – исходная матрица факторных нагрузок; Т – матрица преобразований.

Элементами каждой матрицы преобразований являются sin β и cos β. Исходя из геометрического представления процесса вращения β – это угол, на который поворачивается пара факторов в пространстве. Следует подчеркнуть, что в процессе вращения величина общности по каждому признаку остается неизменной.

Таким образом, применение факторного анализа при исследовании экономических процессов является одной из наиболее актуальных задач экономико-математических исследований.

Библиографическая ссылка