Одна из причин непонимания математики – пассивность учащегося. Обязанность каждого преподавателя – стимулировать познавательную активность студентов. Этого возможно добиться, если повысить интерес к изучению математики, показывая ее многочисленные приложения к решению различных задач механики, физики, биологии, экономики, знакомя с новыми направлениями в естествознании, возникающими на стыке математических и естественнонаучных дисциплин. Активность студентов можно повысить стимуляцией самостоятельной работы, требующую от них интеллектуальных усилий и продуктивных действий, направленных на развитие мышления, памяти, творческих способностей. К примеру, студентам предлагается самим найти тему для доклада на занятии, которая их заинтересует и поможет повысить интерес к изучаемому предмету. В нашей работе мы рассмотрели тему «Золотое сечение»
Люди различают предметы, которые его окружают по форме. Интерес к какому-либо предмету может быть вызван жизненной необходимостью или красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наиболее лучшему зрительному восприятию красоты и гармонии. Целое состоит из частей, а части находятся в определенном отношении друг к другу и к самому целому. Принцип золотого сечения – это высшее проявление структурного и функционального совершенства целого и его частей в науке, природе, технике и искусстве.
Геометрический смысл «золотого сечения» состоит в пропорциональном делении отрезка на неравные части. При этом отрезок так относится к большей части, как большая часть относится к меньшей.
Построение «золотого сечения» осуществляется с помощью линейки и циркуля.
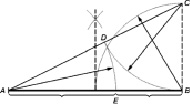
Из точки В откладывается перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Начнем с алгебраических свойств «золотой пропорции». Из уравнения «золотой пропорции» x2 = x + 1 непосредственно вытекает первое очень простое и тем не менее весьма удивительное свойство золотой пропорции:
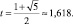
Если корень t подставить вместо x в уравнение, то мы получим следующее тождество для «золотой пропорции»:
t2 = t + 1.
Убедимся, что данное выражение истинно. Для этого нужно осуществить элементарные математические преобразования над левой и правой частями тождеств и доказать, что они совпадают. Мы имеем для правой части:
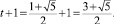
Второе тождество может быть представлено в виде:
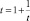 или
или 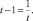 .
.
Теперь рассмотрим примеры «золотого сечения». Одним из них может являться правильный пятиугольник – выпуклый и звездчатый. внутри него можно продолжить строить пятиугольники, и данное отношение будет сохраняться. Звездчатый пятиугольник называется пентаграммой. Пятиконечная звезда была выбрана пифогорейцами в качестве талисмана, который считался символом здоровья и служил опознавательным знаком.
На основании пропорции золотого сечения был построен ряд чисел, замечательный тем, что каждое последующее число оказывалось равным сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 1З, 21 и т.д. Этот ряд был открыт итальянским математиком Фибоначчи и называется поэтому рядом Фибоначчи. Он обладает тем свойством, что отношения между соседними членами по мере возрастания чисел ряда, все более приближаются к 0,618, то есть, к отношению золотого сечения.
В прямоугольнике золотого сечения стороны находятся в отношении золотого сечения. Этот прямоугольник содержит в себе квадрат и малый прямоугольник золотого сечения (его большая сторона является малой стороной первоначального прямоугольника).
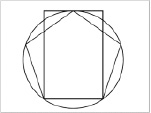
Поэтому можно построить прямоугольник золотого сечения на основании квадрата: сторона квадрата делится пополам, из той точки к вершине проводится диагональ, с помощью которой на стороне квадрата строится прямоугольник золотого сечения
Этот малый прямоугольник подобен большому прямоугольнику, составленному из квадрата и малого прямоугольника золотого сечения, то есть оба эти прямоугольника являются прямоугольниками золотого сечения. Разбивая этот меньший прямоугольник на квадрат и еще меньший прямоугольник, мы опять получим прямоугольник золотого сечения, и так до бесконечности. Если соединить вершины квадратов кривой, то мы получим логарифмическую кривую, бесконечно растущую спираль, которую называют «кривая развития», «спираль жизни», ибо в ней как бы заложена идея бесконечного развития.
Бесконечное повторение прямоугольника золотого сечения и квадрата при рассечении прямоугольника золотого сечения обнаруживает повторение целого в его частях, что является одним из условий гармонии целого. Это свойство прямоугольника золотого сечения было обнаружено художниками и они стали употреблять золотое сечение как способ гармонизации, способ пропорционирования.
В искусстве и архитектуре прославленные свойства золотого сечения используются с большим успехом. Размеры царской усыпальницы Великой Пирамиды в Египте основаны на золотой пропорции. Этим же соотношением пользовался при создании своих архитектурных шедевров архитектор Ле Корбюзье. Число «фи» нашло отражение в работах художника Пита Мондриана. В своих картинах его использовал великий художник Леонардо да Винчи. Он широко использовал золотую пропорцию в своих творениях, проявляя интерес к присутствию математики в произведениях искусства и природе.
Подобно древнегреческим математикам, Леонардо проводил исследование пропорций человеческого тела, показав, как главные его части соотносятся с числом «фи». На незаконченной картине великого художника «Святой Иероним» изображен мыслитель, человек, сделавший перевод Ветхого Завета с еврейского на латинский. Полагают, эта картина была нарисована специально для того, чтобы убедиться: центральная фигура святого вписывается в так называемый золотой прямоугольник.. Учитывая любовь Леонардо к «геометрическим забавам», это предположение кажется вполне оправданным. Лицо всемирно известной Моны Лизы идеально вписывается в золотой прямоугольник.
Художники, ученые, модельеры, дизайнеры делают свои расчеты, чертежи или наброски, исходя из соотношения золотого сечения. Пропорции различных частей тела человека составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными. Принцип расчета золотой меры на теле человека можно изобразить в виде схемы: M/m = 1,618/
Множество примеров золотого сечения кроется в чертах лица. Однако точные соответствия формуле золотого сечения, по мнению ученых и людей искусства, художников и скульпторов, существуют только у людей с совершенной красотой. Собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора.
К примеру, сложив ширину двух передних верхних зубов и разделив эту сумму на высоту зубов и получив при этом число золотого сечения, можно утверждать, что строение таких зубов идеально.
В ходе работы были раскрыты алгебраические и геометрические свойства золотой пропорции. Рассмотрев произведения изобразительного искусства, скульптурного мастерства, созданные с использованием золотой пропорции, мы убедились в её значимости в самых разных областях нашей жизни.
Библиографическая ссылка
Мелешко С.В., Беляева Е.Д., Куксова Е.В. ЗОЛОТОЕ СЕЧЕНИЕ В МАТЕМАТИКЕ И ДРУГИХ ОБЛАСТЯХ // Современные наукоемкие технологии. 2013. № 6. С. 78-79;URL: https://top-technologies.ru/ru/article/view?id=31990 (дата обращения: 02.03.2026).



