При построении динамических математических моделей различных процессов и устройств широкое применение получают дифференциальные уравнения. При этом, сам процесс имитационного математического моделирования, исследования модели представляет собой, по сути, решение этих дифференциальных уравнений при различных начальных условиях, параметрах уравнения и вариациях правой части [1].
Весьма удобными инструментами для выполнения указанных исследований представляются современные математические пакеты, в которых реализован принцип так называемого визуального программирования. При использовании таких пакетов исследователь строит схему моделирования из стандартных блоков библиотеки, в которую включает источники сигналов, непосредственно исследуемую модель и средства отображения результатов моделирования. При этом, в отличие от классических способов моделирования, исследователю не нужно изучать язык программирования, используемые численные методы математики, а достаточно лишь общих умений работы на компьютере и, собственно, сути исследуемого процесса [3].
Система вычислений MATLAB и ее составляющая среда визуального моделирования Simulink по праву являются одними из наиболее распространенных пакетов для технических и математических вычислений, в которых реализован описанный принцип визуального программирования. В качестве примера рассмотрим решения весьма распространенного в различных областях знаний линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами следующего вида [2]:
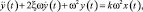(1)
где x(t) – входной сигнал системы, как заданная функция времени; y(t),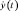 
, 
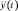– решение уравнения и его производные; k, ω, ξ – постоянные коэффициенты уравнения.
Исследование решений уравнения (1) в среде визуального моделирования Simulink системы MATLAB для различных входных воздействий выполним с использованием схемы моделирования, представленной на рис. 1. Центральное место на рассматриваемой схеме занимает собственно модель дифференциального уравнения в форме передаточной функции, которая получается применением к нему преобразования Лапласа
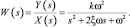(2)
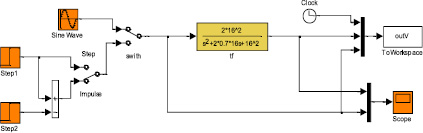
Рис. 1. Схема моделирования
Диалоговое окно, для ввода и изменения параметров уравнения имеет вид, показанный на рис. 2.
Левая часть схемы моделирования содержит переключаемые источники задающих воздействий, соответствующих различным правым частям уравнения . В частности представлены источники ступенчатого, импульсного и гармонического воздействий, параметры которых также легко редактируются.
Процесс решения уравнения сводится к запуску моделирования и просмотру его результатов на своеобразном экране (Scope). На рис. 3 приведены результаты моделирования уравнения для значений параметров, указанных на рис. 1 для импульсного воздействия.
Таким образом, визуализация решений дифференциальных уравнений в среде визуального моделирования Simulink системы MATLAB делает процесс исследования математических моделей на их основе предельно простым и наглядным.
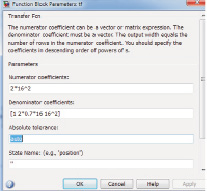
Рис. 2. Диалоговое окно редактирования параметров уравнения
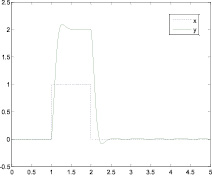
Рис. 3. Результаты моделирования уравнения для импульсного воздействия
Библиографическая ссылка
Литвин Д.Б., Дроздова Е.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В СРЕДЕ ВИЗУАЛЬНОГО ПРОГРАММИРОВАНИЯ // Современные наукоемкие технологии. – 2013. – № 6. – С. 77-78;URL: https://top-technologies.ru/ru/article/view?id=31989 (дата обращения: 16.04.2024).