Ф. Энгельс заметил, что лишь дифференциальное исчисление дает возможность математически изображать процессы, движение. Поэтому целью данной работы является выяснить роль производной в экономике.
Производная является основным понятием дифференциального исчисления, которая характеризует скорость изменения функции. Производной функции y = f(x)в точке x0 называют предел отношения приращения функции к приращению аргумента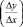 
, когда ∆x → 0. Функция, имеющая производную, называется дифференцируемой. Производная обозначается y’(x0) или f’(x0).
Определение производной выражается с помощью формулы:
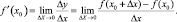
На вопрос «что такое производная?» экономист ответит: «Маржинализм».
«Marginal» в переводе с английского означает «предельный». Предельными величинами в экономике являются: предельный доход, предельные издержки, предельная полезность, предельная производительность труда. Они характеризуют не состояние, а процесс, т.е. изменение экономического объекта. Поэтому производная показывает скорость изменения некоторого экономического объекта или процесса с течением времени или по отношению к другому исследуемому фактору.
Пусть q – выпуск произведенной продукции, TC(q) – соответствующие данному выпуску издержки производства (total costs), ∆q – прирост продукции, а DТС – прирост издержек произодства.
Предельные издержки МС (marginal costs) показывают дополнительные затраты на производство дополнительной единицы продукции:
MC = TC(q + ∆q) – TC(q),
где ∆q = 1
Так как ∆TC ≈ dTC, то получим MC = ∆TC ≈ dTC = TC’(q)∆q = TC’(q).
Подпредельным (маржинальным) значением показателя в экономическом анализе понимают производную функции этого показателя.
Для исследования процессов в экономике применяют понятие эластичности функции (Ex,y), которое показывает предел отношения относительного приращения функции y к относительному приращению переменной x, при ∆x → 0:
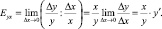
Эластичность функции – это изменение одного показателя x по отношению к изменению другого показателя y, от которого зависит первый. Она показывает процентное изменение одной переменной в результате изменения другой на 1 %.
Существует несколько видов эластичности:
– Эластичность спроса по цене (прямая):
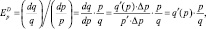
она показывает процентное изменение величины спроса на какое-либо благо при изменении его цены на 1 % и характеризует реакцию потребителей на изменение цен на продукцию.
Если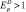 
, то спрос является эластичным (или относительно эластичным). Объём спроса изменяется на больший процент, чем цена.
Если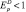 
, то спрос называется неэластичным. Объем спроса меняется на меньший процент, чем цена.
Если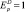 
, то говорят, что товар имеет единичную эластичность и изменение цены вызывает абсолютно пропорциональное изменение объема спроса.
Если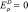 
, то спрос на данный товар называется абсолютно неэластичным. Объем спроса не меняется при изменении цены и остается постоянным при любом её изменении.
Если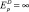 
, то спрос называется абсолютно эластичным. Объем спроса неограничен при падении цены ниже определенного уровня.
– Эластичность спроса по доходу:
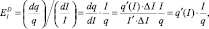
характеризует относительное процентное изменение величины спроса на какое-либо благо при изменении дохода потребителя на 1 %. Положительная эластичность определяет качественные товары, а отрицательная – некачественные.
– Ценовая эластичность ресурсов:
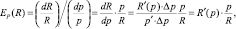
показывает относительное изменение величины спроса на какой-либо ресурс, например, труд, при изменении его цены на 1 %.
Производную используют при решении экономических задач:
Задача № 1. Пусть функция спрoca имеет вид QD = 100 – 20p, пocтоянные издержки TFC (total fixed costs) cocтавляют 50 денежных единиц, а переменные издержки TVC (total variable costs) на производство единицы продукции – 2 денежныe единицы. Найти объём выпуска, максимизирующий прибыль монополиста.
Решение: Рассчитаем прибыль:
П = TR – TC,
где TR = pQ; TC = TFC + TVC.
Цена eдиницы продукции:
20p = 100 – Q ⇒ p = 5 – Q/20,
тогда
П = (5 – Q/20)Q – (50 + 2Q) = = – 2Q + 60Q – 1000 → max
Значит объём выпуска П′(Q) = –2Q + 60 достигнет максимума при равенстве нулю производной по цене:
–2Q + 60 = 0 ⇒ Q = 30.
Задача № 2. Цементный завод производит Х т цемента в день. По договору он должен
ежедневно поставлять строительной фирме не менее 20 т цемента. Производственные мощности завода таковы, что выпуск цемента не может превышать 90 т цемента в день.
Определить, при каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид:
K = –x3 + 98x2 + 200x,
а удельные затраты составят:
K/x = –x2 + 98x + 200 .
Решение: Найдем наибольшее и наименьшее значение функции y = –x2 + 98x + 200 на промежутке [20; 90].
Выведем x = 49 – критическая точка функции. Найдем значение функции на концах и в критической точке: f(20) = 1760; f(49) = 2601; f(90) = 320.
Итак, при выпуске 49 т цемента в день удельные издержки максимальны (т.е экономически это не выгодно), а при выпуске 90 т в день удельные издержки минимальны, значит заводу можно работать на предельной мощности и ещё более усовершенствовать свои технологии, поскольку дальше начнет действовать закон убывающей доходности и без нововведений выпуск продуции не может быть увеличен.
На мой взгляд, производная является важнейшим инструментом экономического анализа, который позволяет углубить математический смысл экономических понятий и выразить экономические законы с помощью математических формул. Экономический смысл производной состоит в том, что она выступает как скорость изменения некоторого экономического процесса с течением времени или по отношению к другому исследуемому фактору. Многие законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем.
Библиографическая ссылка
Кочержова Е.Н., Боташева Л.Р., Цыплакова О.Н. РОЛЬ ПРОИЗВОДНОЙ В ЭКОНОМИКЕ // Современные наукоемкие технологии. – 2013. – № 6. – С. 72-74;URL: https://top-technologies.ru/ru/article/view?id=31986 (дата обращения: 21.11.2024).