Современный экономист должен хорошо владеть количественными методами анализа. К такому выводу нетрудно прийти практически с самого начала изучения экономической теории. При этом важны как знание традиционных математических курсов (математический анализ линейная алгебра, теория вероятностей), так и методов, применяемых в практической экономике и экономических исследованиях (математическая и экономическая статистика, исследование операций, теория игр, эконометрика и др.). Математика является не только орудием количественного расчета, но также методом точного исследования. Она служит средством предельно четкой и ясной формулировки экономических понятий и проблем. Рассмотрим возможности использования понятия интеграла при решении экономических задач и описании экономических явлений.
Рассмотрим функцию у = g(x), характеризующую неравномерность распределения доходов среди населения, где у – доля совокупного дохода, получаемого долей х беднейшего населения. График этой функции называется кривой Лоренца (Макс Лоренц (1876–1959) – американский экономист и математик) (рисунок).
Очевидно, что 0 ≤ g(x) ≤ xпри х ∈ [0; 1], и неравномерность распределения доходов тем больше, чем больше площадь фигуры. В связи с этим в качестве меры указанной неравномерности используют так называемый коэффициент Джини k (Джини Корадо (1884–1965) – итальянский экономист, статистик), равный отношению площади фигуры ОАВ к площади треугольника ОАС. Рассмотрим пример.
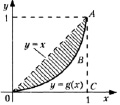
Рис. 1
По данным исследований о распределении доходов в одной из стран кривая Лоренца ОВА (см. рисунок) может быть описана уравнением
,
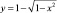где х – доля населения; у – доля доходов населения. Вычислить коэффициент Джини.
Очевидно, что коэффициент Джини
,
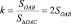так как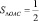 
.
Далее
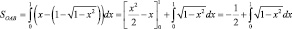
Интеграл вычислим с помощью тригонометрической подстановки
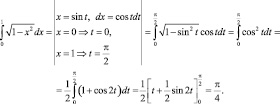
Тогда коэффициент Джини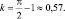 
Достаточно высокое значение k показывает существенно неравномерное распределение доходов среди населения в рассматриваемой стране.
Определение начальной суммы по ее конечной величине, полученной через время t (лет) при годовом проценте (процентной ставке) р, называется дисконтированием. Задачи такого рода встречаются при определении экономической эффективности капитальных вложений.
Пусть Kt – конечная сумма, полученная за t лет, и K – дисконтируемая (начальная) сумма, которую в финансовом анализе называют также современной суммой. Если проценты простые, то K = Kt (1 + it), где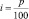 
– удельная ставка процента. Тогда 
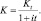В случае сложных процентов K = Kt (1 + it)t, поэтому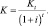 
Пусть поступающий ежегодно доход изменяется во времени и описывается функцией f(t) и при удельной норме процента, равной i, процент начисляется непрерывно. Можно показать, что в этом случае дисконтированный доход К за время Т вычисляется по формуле
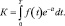
Рассмотренные примеры позволяют сделать вывод о том, что интегральное исчисление является мощным средством, как при решении прикладных экономических задач, так и для описания таких понятий экономической теории как коэффициент Джини, дисконтирование и многих других. Конечно, сегодня при решении экономических задач повсеместно используются специализированные программные продукты, позволяющие производить расчеты быстро и точно. Но наличие компьютерных технологий не отменяет необходимости оперирования фундаментальными знаниями, если речь идет о специалисте высокой квалификации, который готов решать сложные задачи, предлагая нестандартные решения.
Библиографическая ссылка
Иващенко Е.В., Богомольский С.А. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ В ЭКОНОМИЧЕСКОЙ ТЕОРИИ // Современные наукоемкие технологии. – 2013. – № 6. – С. 68-69;URL: https://top-technologies.ru/ru/article/view?id=31984 (дата обращения: 21.11.2024).