Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы
• Ключевые слова
• Литература

Гулай Т.А. 1 Квеквескири Е.Н. 1 Камова К.А. 1

---

1 Ставропольский государственный аграрный университет

Статья в формате PDF

421 KB

1. Леонтьев В.В., Форд Д. // Экономика и математические методы. – 1972. – № 3.

2. Стеценко В.Я. Модель Леонтьева – Форда межотраслевого баланса, учитывающая экологический фактор. – Тамбов, XV Международная научная конференция «Математические методы в технике и технологиях», 2002. – Т 5. – С. 154–157.

3. Красносельский М.А., Вайникко Г.М., Забрейко П.П., Рутицкий Я.Б., Стеценко В.Я. Приближенное решение операторных уравнений. – М.: Наука, 1969. – 455 с.

4. Колодяжная Т.А., Гробова Т.А. Применение теоремы о средних величинах при доказательстве неравенств. – Ставрополь, Научно-инновационные достижения СМС в области физико-математических наук и технических дисциплин. – 52 научно-методическая конференция. – 2007. – С. 128–131.

Значительное число задач анализа, алгебры, теории интегральных уравнений можно представить с единых позиций в виде линейного или нелинейного операторного уравнения вида:

x = A(x) + f (1)

с оператором A(x), действующим в том или ином пространстве Е. При этом для таких уравнений возникают весьма специфические задачи. В качестве довольно распространенных задач такого типа, например, встречается задача о существовании у таких уравнений решения x = x*, обладающего свойством неотрицательности: x* ≥ θ. Такого рода задачи, вообще, специфичны в задачах экономики, для которых экономический смысл имеют лишь неотрицательные решения (типичный пример – модель Леонтьева межотраслевого баланса).

Поэтому при рассмотрении подобных задач предполагается наличие в пространстве дополнительной структуры–конуса К, с помощью которого в пространстве Е вводится полуупорядоченность: для некоторых пар векторов x, y ∈ E определено отношение x ≥ y, являющееся аналогом обычного скалярного неравенства: x ≥ y если (x – y) ∈ K. От свойств конуса в пространстве Е и оператора А, действующего в этом пространстве зависит существование решения x* у уравнения (1), а также способ, с помощью которого можно построить приближения к этому решению. Загрязнение окружающей среды – побочный продукт обычной экономической деятельности.

Побочные продукты (как ценные, так и неценные) непосредственно связанны с системой физических взаимодействий, определяющих повседневное функционирование экономической системы. Техническую взаимозависимость между уровнями выпуска желательных и нежелательных продуктов, можно описать в терминах коэффициентов, которые используются для выявления взаимозависимости между всеми обычными отраслями производства и потребления. Поэтому побочные продукты производственной деятельности и потребления следует рассматривать как часть экономической системы. Модель, учитывающая экологический фактор известна как модель Леонтьева-Форда [1]:

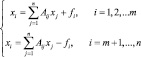
Рассмотрим статистическую линейную модель межотраслевой экономики, – модель Леонтьева. В ее основе лежат следующие предположения:

1) в экономической системе производятся, продаются, покупаются, инвестируются n – продуктов;

2) каждая отрасль является «чистой», т.е. производит только один продукт;

3) под производственным процессом в каждой отрасли понимается преобладание некоторого, а возможно и всех типов продуктов в определенном количестве.

При этом соотношение затраченного продукта и выпускаемого находятся в постоянном отношении.

Если для производства единицы i-продукта надо затратить aij j-продукта, то выпуск x-единиц i-продукта потребует aijx единиц j-го.

Независимо от масштаба производства удельный выпуск и соотношение затрат представляются const.

При валовом выпуске x затраты i-продукта на все остальное производство составят 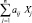, тогда «чистый» выпуск должен быть не меньше, чем спрос на соответствующий продукт:

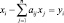(i = 1,2…n), (2)

где yi – спрос.

(2) – модель Леонтьева межотраслевого баланса [1]. Конечный спрос состоит из конечного потребления экспорта и инвестиций. Однако в модели он представляется заданным и требуется найти такой валовой выпуск для каждой отрасли, которая обеспечит заданный конечный спрос.

Сущность модели Леонтьева состоит в определении валового выпуска отраслей по заданному конечному спросу на основе данных о технологических возможностях [1]. Коэффициенты aij – называются технологическими, а матрица A = (aij) – технологическая или производственная матрица.

Наряду с моделью Леонтьева рассматривают более общую задачу – модель Леонтьева – Форда. Эта модель имеет вид

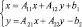(3)

и является моделью производства, в котором: вектор x ∈ Rn, x ∈ q является вектором валового выпуска полезного продукта; y ∈ Rm, y ∈ q – вектор вредных отходов в окружающей среде, возникающих, в частности, в процессе производства, подлежащих «уничтожению» с целью понижения содержания вредных продуктов до экологически обусловленного заданного уровня; b2 ∈ Rm, b1 ∈ Rn – вектор чистого выпуска полезного продукта, A11 – (n×n) технологическая матрица, т.е. A11x – выражает вектор затрат полезного продукта при валовом выпуске вектора x; A12 – (n×m) матрица, такая, что A12y – вектор затрат полезного продукта на уничтожение вредных отходов в «объеме» вектора y; A21 – (m×n) матрица такая, что при выпуске валового вектора x полезного продукта в окружающую среду выделяется вектор A21x вредных отходов, A22 – (m×m) матрица, такая, что A22y – вектор вредных отходов, дополнительно возникающих при «уничтожении» вектора y вредных отходов.

Теоремы, доказанные Стеценко В.Я. [2], позволяют получать априорные оценки решения уравнения

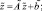(4)

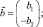
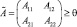
на основе результатов по ускорению сходимости приближений к решению операторного уравнения [4] и [3].

Библиографическая ссылка