Тот, кто хочет решить вопросы естественных наук без помощи математики, ставит неразрешимую задачу. Следует измерять то, что измеримо, и делать измеримым то, что таковым не является.
Галилео Галилей
Математика является наукой, располагающейся на границах естествознания. Поэтому естествознание все чаще прибегает к математическим методам для истолкования законов природы. Толкование какого бы то ни было явления является настоящим, только в том случае, если удалось создать математический аппарат передающий логичность данного процесса.
Естествознание использует математику в следующих направлениях: во-первых с помощью математики производится количественный анализ и формулировка установленных фактов, во-вторых строятся математические модели, рождается математическая экология, физика и т.д.; и, наконец, формулируется язык научных теорий.
Области применения математики практически не ограничены. Математика и естествознание тесно связаны. На конкретном этапе развития естественнонаучных дисциплин возникает необходимость их математизации. Даже простейшие математические операции служат отправной точкой естествознания. Наука использует её для того чтобы «создавать мосты» для перехода от эмпирических методов исследования к рациональным, для развития различных концепций и представлений в естествознании. Ценность математических методов заключается в том, что она способна легко переходить из одной области знания в другую, благодаря абстрагированию от определенных свойств объектов. Но следует учитывать то, что математика исследует не саму природу, а лишь математические модели и прообразы окружающей нас действительности.
Для того, чтобы выделить наиболее универсальные, важные признаки, характерные различным научным системам, применяется математическое моделирование. Модели математики применяются в том случае, когда экспериментальное изучение требует значительных расходов или же совсем немыслимо.
С помощью математического моделирования мы получаем ответы на многие интересующие нас вопросы. Процесс создания математических моделей можно представить в виде следующих ступеней: во-первых необходимо выразить основные вопросы, ответы на которые мы ищем; затем происходит поиск информации об изучаемом объекте; следующим шагом намечаются цели моделирования; на следующем этапе отмечаются наиболее важные признаки моделируемого объекта, формализуются главные характеристики ; после вырабатываются принципы работы с ними. Так и зарождается математическая модель. Далее происходит её исследование с применением аналитических и вычислительных методов, сопровождающихся в конечном счете нахождением ответов на поставленные вопросы. Если модель безупречна, то полученные данные о модели бывают подобны данным об исследуемой системе.
Особенностью моделирования в естествознании является возможность объединения качественных и количественных методов анализа. Математическая модель способна не только пояснять характеристики изучаемого объекта, но и прогнозировать его новые свойства. Кроме этого она помогает устанавливать взаимосвязи между, казалось бы, совсем не связанными между собой явлениями, способствует упорядочению фактов. Следует также отметить, что масштабы применения математического моделирования в естествознании весьма велики, и можно даже сказать не ограничены. В качестве примера можно привести использование моделей математики в экологии.
Моделирование развития изолированной популяции с дискретным размножением с учетом внутривидовой конкуренции.
Необходимо рассмотреть биологические виды, для которых потомки и предки не сосуществуют во времени (многочисленные растения, насекомые и др.). Тогда последовательные значения численности популяции можно представить N0, N1, ...
Если нет никаких причин ограничения численности популяции, тогда возникает простейшая модель:
Nt + 1 = R∙Nt
где R – коэффициент воспроизводства.
Решение этой модели очевидно:
Nt = N0∙Rt
и при R > 1 численность популяции нарастает по геометрической прогрессии.
Даже эта простейшая модель заслуживает обсуждения. Она выражает то, что в литературе иногда называют «законом Мальтуса».
Понятно, что бесконечно долго увеличиваться популяция не может. Наипростейший способ учета внутривидовой конкуренции основывается на том, что коэффициент воспроизводства не является постоянной величиной, а зависит от числа особей в популяции, уменьшаясь по мере ее роста. Таким образом, необходимо брать в расчет, что величина R монотонно уменьшается с ростом величины N. Реального характера этого спада мы не знаем; его можно представить множеством способов с использованием общеизвестных элементарных функций.
Модель, в основу которой положена простейшая из таких функций, выглядит следующим образом:
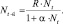
Полезность заключается в том, что описываемое ею поведение численности популяций неоднократно наблюдалось экологами в природе.
Далее следует рассмотреть модель, показывающую четыре абсолютно разных типа динамики численности популяций (в зависимости от соотношения значений параметров): монотонное возрастание с выходом на стационар, колебательное установление численности, регулярное колебательное изменение (так называемые «предельные циклы») и хаотическое поведение без каких-либо видимых закономерностей. Все эти типы динамик наблюдаются в природе.
При изучении моделей, выраженных дифференциальными уравнениями, методика исследования в основном одинакова. Она представляет собой следующую последовательность:
- определение проблемы, введение терминологии, описание поведения определенных природных систем;
- создание математической модели;
- попытка качественного изучения модели, включая построение диаграмм на фазовой плоскости параметров модели;
- численное решение дифференциальных уравнений (как правило, простейшими из методов дискретизации, либо путем использования готовых программ).
Одна из основных задач математики в естествознании заключается в создании специализированного языка данной науки. Без сомнений можно говорить о том, что математический язык является многофункциональным и универсальным языком естествознания. Недаром немецкий математик Г.Вейль писал «... Все законы выводятся из опыта. Но для выражения их нужен специальный язык. Обиходный язык слишком беден, кроме того, он слишком не определен для выражения столь богатых содержанием точных и тонких соотношений. Таково первое основание, по которому физик не может обойтись без математики; она дает ему единственный язык, на котором он в состоянии изъясняться».
С помощью формул, уравнений и логического аппарата можно гораздо проще выразить сложные процессы происходящие в природе; благодаря ему можно точно дать определения количественным закономерностям, присущим изучаемым явлениям. Математический язык исключает неопределенность. Он очень лаконичен и ёмок. Его понятия и термины можно употреблять для обозначения самых разнообразных явлений окружающего нас мира. Данные преимущества свидетельствуют о том, что существуют прочные связи между языком математики и языком качественных описаний. Чем большей информацией о качественных свойствах явлений мы располагаем, тем эффективнее становится применение математических методов исследования, и наоборот, чем совершеннее количественные методы, тем лучше исследуются их качественные особенности.
Но у каждой медали есть и оборотная сторона. Математическому языку также присущи некоторые недостатки. Конечно, с помощью него можно описать количественно все явления и процессы на земле, но все же математика «убивает индивидуальность», как выразился российский математик И.Шафаревич, то есть не уделяется должное внимание богатству качественных проявлений мира. В математическом подходе описывается лишь какой-либо определенный аспект изучаемого явления, а остальные признаки опускаются. Математические формулы абстрактны и не имеют однозначного содержания. Но этот недостаток обусловлен тем, что математика не может функционировать иначе, необходимо все-таки помнить о рамках использования этой науки.
В современном мире роль математики в естествознании усиливается. Зачастую теоретические данные о каком-либо объекте являются неполноценными, пока не будет создано доказательство, основанное на математических методах, обосновывающих логику данных явлений и объектов.
Вселенная функционирует по законам математики в большей, чем мы предполагаем, мере. Вот почему эта наука сохраняет непреходящую ценность уже на протяжении долгих лет.
Библиографическая ссылка
Абдулжалиева А.К., Долгополова А.Ф. ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ В ЕСТЕСТВОЗНАНИИ // Современные наукоемкие технологии. 2013. № 6. С. 64-65;URL: https://top-technologies.ru/ru/article/view?id=31980 (дата обращения: 02.03.2026).



