Постановка проблемы: поставить и аналитически решить одну из возможных оптимизационных задач пассивного кооперативного взаимодействия двухпродуктовых развивающихся систем (РС).
Актуальность поставленной проблемы. Решение поставленной проблемы позволит наилучшим образом распределять внешний ресурс между такими двумя взаимодействующими РС, у которых обмен между собой продуктами их деятельности отсутствует (в этом случае системы будем называть пассивно взаимодействующими).
Анализ последних исследований и публикаций. Академик В.М. Глушков при изучении макроэкономических задач ввел новый класс математических моделей, который в дальнейшем стал применяться при моделировании не только экономических, но и биологических, экологических и др. систем [6]. В дальнейшем были поставлены и решены многие теоретические и прикладные задачи моделирования развивающихся (или эволюционирующих [8]) систем [1,7-10]. Приведем определение РС, придерживаясь [7, с. 21-22], [6, с. 9-10], [2, с. 87-89] (строгое определение РС, как отмечается в [6, с. 12], представляется нецелесообразным). Пусть система состоит из отдельных элементов, выполняющих различные определенные функции. Эти элементы будем отличать временем их создания и показателями эффективности выполнения функций. По функциональному признаку система делится на подсистемы, элементы которых выполняют однотипные функции. Будем различать внутренние и внешние функции системы. Внутренние функции обеспечивают функционирование, совершенствование и развитие самой системы, например производство новых элементов системы, повышение эффективности создаваемых элементов и т.п. Внешние функции обеспечивают основную, главную функцию системы, например выпуск некоторых обобщенных внешних (для данной системы) продуктов. Рассматриваемая нестационарная система обладает переменной структурой, под которой понимается распределение функционирующих элементов системы по времени их появления в системе, выполняемым функциям и эффективности их выполнения. В системе происходит обновление элементов: вводятся в действие новые, более эффективные элементы и ликвидируются самые старые (неэффективные) элементы. Эти новые элементы могут создаваться внутри системы (в одной из подсистем совершенствования системы) или поступать в систему извне. В момент начала развития либо должно быть наличие в системе определенных первоначальных ресурсов либо система, не обладающая такими ресурсами, должна обладать способностью получать из внешней среды ресурсы и воспроизводить их (такая РС называется возникающей РС [1]). В систему должны поступать вещество, энергия и информация. Должен быть учтен характер условий внешней среды, во взаимодействии с которой система создает и потребляет продукты, а также выделяет устаревшие ненужные продукты в «отвал». Должны выполняться некоторые балансовые соотношения между субстратами, поступающими в систему, и продуктами системы, причем должна быть функциональная связь между ресурсами, затрачиваемыми на внутреннее развитие и на выполнение внешних функций системы, между скоростью воспроизводства ресурсов, интенсивностью их использования и результатами функционирования системы.
Теперь допустим, что относительно рассматриваемого объекта моделирования (типа РС) нас интересуют только две его функции: первая (внутренняя), обеспечивающая его существование и развитие, и вторая (внешняя), являющаяся результатом его взаимодействия с внешней средой. Материальное, энергетическое и информационное обеспечение первой функции назовем продуктами первого рода, второй –продуктами второго рода. Примерами в экономике продуктов 1-го и 2-го рода могут служить соответственно рабочие места и продукты потребления и услуги, в биологии – реакционные (активные) центры и внешние результаты взаимодействия обособленного объекта с внешней средой. Всю систему представим в виде двух подсистем А и Б. Подсистема А (подсистема самосовершенствования системы) при помощи одной части ранее появившихся (созданных и поступивших извне) продуктов 1-го рода создает новые продукты 1-го рода, подсистема Б (подсистема выполнения основной функции РС) создает и принимает извне новые продукты 2-го рода (для макроэкономической системы А – группа производства средств производства, Б – группа производства предметов потребления, каждая со своим рабочим местом). Внутренними ресурсами РС будем считать продукты только первого рода, являющиеся источниками самих себя и продуктов второго рода. Внешними ресурсами РС будем называть продукты как первого, так и второго рода, поступающие в РС из внешней среды (при этом часть внешних ресурсов становится внутренними ресурсами РС). Внешние ресурсы и продукты 1-го рода в дальнейшем предполагаются приведенными к одной размерности. Вышеописанную РС будем назвать двухпродуктовой РС. Рассматривались и изучались также многопродуктовые РС [6-10] и континуальные РС (в случае, когда продуктов бесконечно много) [5-10].
Главной особенностью интегрального аппарата В.М. Глушкова, применяемого при моделировании РС, являлось:
1) наличие функции (заданной или искомой) в нижних пределах интегралов, интерпретируемой как временная граница ликвидации устаревших технологий производства продуктов;
2) наличие функции в подынтегральных выражениях, с помощью которой можно было изменять распределение ресурсов между подсистемами, а, значит, управлять развитием системы.
Глушковым В.М. и Ивановым В.В. была поставлена и качественно решена [6] важнейшая для практики задача отыскания наилучшего распределения ресурсов между подсистемами системы с целью получения наибольшего выхода продуктов системы на некотором плановом временном промежутке. В дальнейшем на основе разделения ресурсов на внутренние и внешние (поступающие в систему извне) в [4] были предложены и в [1] уточнены модели, использующие функции более широкого, чем у Глушкова класса, учитывающие непосредственное воздействие на систему внешней среды и позволяющие изучать системы без начальной предыстории (так называемые «возникающие» системы). В [5] были поставлены и решены некоторые задачи взаимодействия континуальных РC. В [2, 3] для частных случаев двухпродуктовой модели были найдены аналитические решения оптимизационных задач распределения внутренних и внешних ресурсов. На основе ранее полученных решений (теорем) оптимизационных задач был сформулирован в [3] и затем уточнен в [10] закон оптимального развития системы – «закон разумного эгоизмасистемы».
Цель работы. В настоящей работе исследуется один из простейших случаев взаимодействия двухпродуктовых РС – случай пассивного кооперативного взаимодействия, при котором происходит лишь заданное перераспределение внешних ресурсов между системами и не происходит обмена продуктами между системами. Поставлена и решена в частных случаях задача наилучшего распределения внешних ресурсов (при заданном распределении внутренних ресурсов) между РС с целью получения наибольшего выхода на заданном временном промежутке их общего внешнего продукта.
Изложение основного материала. Уравнения и неравенства пассивно взаимодействующих двухпродуктовых РС имеют вид:
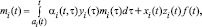(1)
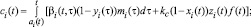(2)
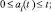
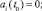
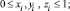
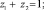
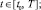
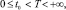
где mi(t) и ci(t) скорости появления в РС с номером i (PCi) в момент времени t новых продуктов соответственно первого и второго родов (в экономической системе продуктами первого рода являются, например, рабочие места, а продуктами второго рода – продукты потребления и услуги, идущие внешнему «заказчику»); f(t) – скорость поступления внешних ресурсов в момент t в обе РС (f и m предполагаются одной размерности, kc – коэффициент согласования размерности f и c); zi(t)f(t) – скорости поступления в PCi в момент t ресурсов из внешней среды,
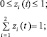
xi(t)zi(t)f(t)и (1 – xi(t))zi(t)f(t) – скорости поступления в PCi в момент t продуктов соответственно первого и второго родов (в подсистемы Ai и Бi соответственно); yi(τ)mi(τ) и (1 – yi(τ))mi(τ) – доли mi(τ), используемые в дальнейшем в PCi для производства соответственно mi(t) в подсистеме Ai и ci(t) в подсистеме Бi, 0 ≤ τ ≤ t, 0 ≤ yi ≤ t; ai(t) – максимальный момент времени, ранее которого появившиеся в PCi продукты первого рода не функционируют по каналам yimi → mi и (1 – yi)mi → ci соответственно в момент t (длина временного интервала t – ai(t) называется продолжительностью последействия или памятью системы), ai(t) ≤ t; αi(t, τ) и βi(t, τ) – скорости создания в момент времени t новых продуктов соответственно первого и второго родов, приходящихся на одну единицу из появившихся в момент τ продуктов первого рода соответственно в подсистеме Ai и в подсистеме Бi, 0 ≤ τ ≤ t; задана начальная предыстория: на промежутке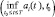 
заданы функции yi(τ) ≡ yi0(τ) и mi(τ) ≡ mi0(τ); t0 – момент начала моделирования РС (PCi называется возникающей, если ai(t) ≥ t0); 0 ≤ t0 ≤ t ≤ T < +∞; все рассматриваемые функции (кроме, быть может, ai(t)) по определению неотрицательны; i = 1, 2
Положим ai(t) ≡ ai(t0) = 0 αi(t, τ) ≡ αi = const > 0, βi(t, τ) ≡ βi = const > 0, 0 < yi = const < 1, i = 1, 2 Уравнения (2) и (3) можно переписать в виде
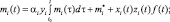(3)
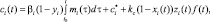(4)
где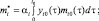 
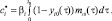
Теорема 1. Если на интервале (0, t0) заданы неотрицательные кусочно-непрерывные функции yi0(τ), mi0(τ) (т.е. задана начальная предыстория), заданы положительные константы αi, βi yi (yi < 1), заданы на отрезке [t0, T], 0 < t0 < T < +∞, непрерывная положительная функция f(t) и кусочно-непрерывные неотрицательные функции xi(t), zi(t), 0 ≤ xi(t), zi(t) ≤ 1 z1(t) + z2(t) = 1, i = 1, 2 то система уравнений (3), (4) имеет на [t0, T] единственное решение
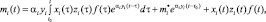
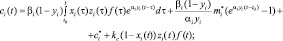(5)
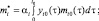
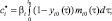t ∈ [t0, T]
причем на [t0, T] функции mi(t) и ci(t) кусочно-непрерывны, i = 1, 2.
Теорему легко доказать совершенно аналогично [3].
Так как теорема 1 справедлива для любых заданных ограниченных и кусочно непрерывных на [t0, T] неотрицательных функций z1(t), z2(t), z1 + z2 = 1 то, положив z ≡ z1, z2 ≡ 1 – z, можно поставить следующую задачу: среди всех заданных кусочно непрерывных функций z(t), 0 ≤ z(t) ≤ 1 найти такую функцию z*(t), которая бы максимизировала функционал
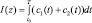
т.е. требуется найти такую z*(t), что
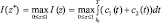(6)
при условии (3), (4).
Теорема 2. В условиях теоремы 1 функционал I(z) принимает вид:
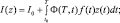(7)
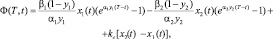
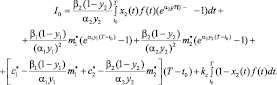
Воспользовавшись теоремой 1 и формулой Дирихле изменения порядка интегрирования в повторных интегралах, требуемый функционал легко вычислить непосредственно подстановкой полученного решения (6).
Теорема 3. Если выполнены условия теоремы 1, то решением поставленной задачи – наилучшим распределением внешних ресурсов между кооперативно взаимодействующими РС, у которых отсутствует обмен продуктами, является
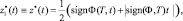
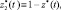t ∈ [t0, T].
Доказательство этой теоремы и нижеследующих выводов (следствий из теоремы 3) непосредственно следуют из вида функционала (7).
Выводы
1. Если выполнены условия теоремы 1, структура и производительности обеих рассматриваемых РС совершенно одинаковы, т.е. x1(t) ≡ x2(t), y1 = y2, α1 = α2, β1 = β2, то любое распределение z*(t), z* ∈ [0, 1], является оптимальным (в том числе и указанное в теореме 3).
2. Если выполнены условия теоремы 1, x2(T) < x1(T) и функция Φ(T, t)непрерывна по переменной t на некотором промежутке (T – ε, T] ⊂ [t0, T], ε > 0 (в частности, если x1(t) и x2(t) непрерывны по t на (T – ε, T)), f(u) > 0 при u ∈ [t0, T] то в силу того, что Φ(T, T) < 0 и непрерывная по переменной t функция Φ(T, t ) сохраняет знак в окрестности точки t = T, для достаточно малого по длине отрезка [t0, T] оптимальное z*(t) ≡ 0, t ∈ [t0, T] т.е. для достаточно малого по длине отрезка временного планирования [t0, T] все внешние ресурсы должны подаваться во вторую РС – в ту РС, в которой относительная доля поступления в момент T внешних ресурсов в подсистему Б (для выполнения внешней функции системы) больше. Очевидно, что указанное утверждение выполняется не только для достаточно малого по длине отрезка [t0, T], но и на конце любого промежутка [t0, T].
3. Если выполнены условия теоремы 1, x2(t) < x1(t), функция Φ(T, t )непрерывна по переменной t на некотором промежутке (T – ε, T] ⊂ [t0, T], ε > 0 f(u) > 0 при u ∈ [t0, T] α1y1 > α2y2 αi > 0 βi > 0 0 < yi < 1, i = 1, 2
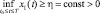
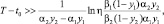
и то для достаточно большой величины T – t0 на большей начальной части отрезка [t0, T]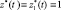 
и лишь в конце этого отрезка 
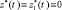, т.е. все внешние ресурсы на большей начальной части отрезка [t0, T] должны подаваться в первую систему и лишь в конце этого отрезка во вторую систему. Этот вывод является для случая пассивного кооперативного взаимодействия двухпродуктовых РС (при заданном распределении между подсистемами каждой системы внутренних и внешних ресурсов и искомом наилучшем распределении между двумя системами внешних ресурсов) аналогом закона оптимального развития системы – «закона разумного эгоизма системы» [3] (при заданном поступлении в систему внешних ресурсов и искомом наилучшем распределении внутренних и внешних ресурсов между подсистемами системы):
1) для достаточно малой величины времени планирования T – t0 искомый оптимум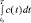 
достигается при максимально возможном (в силу ограничений задачи) использовании в подсистеме Б внутренних и внешних ресурсов для выполнения основной функции системы;
2) для достаточно большой величины времени планирования T – t0 искомый оптимум достигается при существенных долях внутренних и внешних ресурсов, используемых в подсистеме самосовершенствования А на внутренние потребности системы на большей начальной части отрезка времени планирования и максимально возможном использовании в подсистеме Б внутренних и внешних ресурсов для выполнения основной функции системы в конце этого временного отрезка.
Этот закон был выведен из доказанных теорем при достаточно общих предположениях: временная граница ликвидации устаревших технологий – функция a(t)предполагалась искомой, кроме указанных двух уравнений (1) и (2), описывающих функционирование подсистем А и Б, задавалось количество функционирующих в момент времени t продуктов первого рода – непрерывная на [t0, T] функция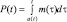 
, непрерывные функции α(t, τ) и β(t, τ), характеризующие наличие научно-технического прогресса, предполагались возрастающими по переменной τ и убывающими по t, (t, τ) ∈ [t0, T)×[ a(t0), T), T ≤ +∞
Библиографическая ссылка
Бугерко Н.В., Гирлин С.К. ОБ ОДНОЙ ЗАДАЧЕ КООПЕРАТИВНОГО ВЗАИМОДЕЙСТВИЯ ДВУХПРОДУКТОВЫХ РАЗВИВАЮЩИХСЯ СИСТЕМ // Современные наукоемкие технологии. – 2013. – № 6. – С. 49-53;URL: https://top-technologies.ru/ru/article/view?id=31971 (дата обращения: 21.11.2024).