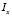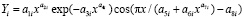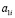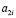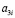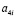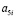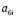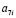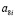Новизна научно-технического решения [1-5] заключается в том, что впервые измерения проводят ниже корневой шейки ствола растущего дерева по форме боковой линии при переходе от ствола к корням, что позволит в будущем подойти к поиску научно-технических решений и по изучению изменений формы корневой части дерева, а также к изучению несимметричных форм комлей различных видов деревьев. Кроме того, научная новизна заключается в том, что впервые получена математическая закономерность влияния максимальной высоты комля берез и других параметров растущих деревьев.
На рис. 1 и 2 приведены схемы реализации способа.
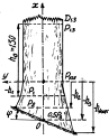
Рис. 1. Схема измерения параметров комля
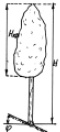
Рис. 2. Схема измерения высоты кроны и дерева
На рис. 1 и рис. 2 приведены следующие условные обозначения: j – угол местного склона в месте произрастания дерева, град; D1.3, P1.3 – диаметр и периметр ствола на высоте 1,3 м от корневой шейки; Pкш – периметр сечения ствола на корневой шейке, см; 0,5 P3 – половина периметра комля березы в сечении над точкой пересечения поверхности почвы с вертикальной осевой линией комля дерева, см; h1 – высота комля березы от корневой шейки до поверхности почвы, см; h2 – высота комля березы от корневой шейки до верхней точки пересечения поверхности почвы с боковой линией комля, см; h3 – высота комля от корневой шейки до центральной точки пересечения поверхности почвы с вертикальной осевой линией комля, см; hmax – максимальная высота комля от корневой шейки до нижней точки пересечения поверхности почвы с боковой линией комля, см; H, Hкр – высоты дерева и кроны, м.
Пример. Для снижения линейной эрозии почвы оврагами применяют растения. Цель исследования – изучение формы комля деревьев, растущих в овраге, для выявления закономерностей взаимодействия между древесными растениями и склоном.
Объектами исследования были выбраны березы на склоне лесного оврага около деревни Ямолино Горномарийского района Республики Марий Эл. Эксперименты были проведены летом 2011 года (табл. 1) на 30 березах.
Таблица 1
Периметры сечения комля на разных высотах (первые 20 берез), см
|
№ березы |
1 |
2 |
3 |
4 |
5 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
Угол j, град |
20 |
18 |
15 |
15 |
15 |
20 |
30 |
20 |
15 |
15 |
20 |
20 |
20 |
15 |
20 |
20 |
20 |
20 |
15 |
|
|
Диаметр D1.3 |
20 |
20 |
15 |
18 |
20 |
20 |
25 |
20 |
35 |
20 |
24 |
20 |
20 |
27 |
28 |
25 |
25 |
42 |
42 |
|
|
Периметр сечения комля |
P1,3 |
85 |
90 |
70 |
70 |
74 |
87 |
75 |
61 |
88 |
56 |
65 |
53 |
62 |
85 |
69 |
76 |
122 |
114 |
91 |
|
Pкш |
87 |
95 |
75 |
80 |
79 |
90 |
85 |
71 |
110 |
72 |
67 |
81 |
75 |
101 |
83 |
98 |
140 |
135 |
110 |
|
|
Р1 |
92 |
81 |
74 |
85 |
80 |
105 |
89 |
75 |
120 |
77 |
76 |
88 |
80 |
105 |
90 |
101 |
147 |
145 |
128 |
|
|
Р2 |
106 |
120 |
80 |
104 |
85 |
96 |
98 |
79 |
125 |
84 |
80 |
90 |
85 |
125 |
93 |
107 |
160 |
153 |
135 |
|
|
Р3 |
140 |
162 |
180 |
140 |
120 |
114 |
116 |
90 |
140 |
102 |
86 |
102 |
98 |
134 |
106 |
116 |
188 |
176 |
150 |
|
|
Высота сечения комля |
h0 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
|
hкш |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
h1 |
–19 |
–27 |
–15 |
–8 |
–6 |
–12 |
–17 |
–17 |
–12 |
–13 |
–18 |
–11 |
–13 |
–16 |
–13 |
–15 |
–16 |
–17 |
–15 |
|
|
h2 |
–40 |
–45 |
–24 |
–15 |
–10 |
–23 |
–30 |
–29 |
–20 |
–21 |
–28 |
–18 |
–20 |
–31 |
–21 |
–28 |
–30 |
–30 |
–22 |
|
|
h3 |
–81 |
–64 |
–60 |
–35 |
–36 |
–40 |
–48 |
–36 |
–40 |
–40 |
–41 |
–35 |
–45 |
–45 |
–40 |
–45 |
–40 |
–43 |
–38 |
|
|
Высота hmax |
–70 |
–66 |
–69 |
–50 |
–40 |
–70 |
–80 |
–90 |
–115 |
–120 |
–115 |
–120 |
–117 |
–130 |
–115 |
–120 |
–105 |
–105 |
–107 |
|
Измерения формы комля (рис. 1) у дерева (рис. 2) по боковой линии поверхности комля выполняется следующим образом.
Сначала определили участок оврага по методике, изложенной в патенте № 2416193 РФ по прототипу, на склоне которого растут деревья. Выбрали учетные деревья для измерений в количестве 30 штук. Для измерений применяли гибкую мерную ленту и транспортир с отвесом. В ходе моделирования идентификацией устойчивых законов было выявлено, что дерево № 6 имеет резко выделяющееся значение угла местного склона. В дальнейшем это наблюдение исключили из статистической выборки.
Данные из таблицы 1 обрабатывали в программной среде CurveExpert-1.3 по модели
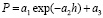 , (1)
, (1)
где P – периметр поперечного сечения комля в разных местах измерения, см; h – высота от поверхности почвы до корневой шейки (в табл. 1 отрицательные значения высоты), а далее до стандартной высоты 1,3 м, см; a2 и a3 – параметры статистической модели (1), причем: a1 – начальное значение периметра комля дерева, см; a2 – активность сбега периметра поперечного сечения комля по боковой линии симметричной формы комля; a3 – постоянный периметр ствола (по условному цилиндру) на высотах от поверхности почвы до нуля на уровне корневой шейки и далее до 1,3 м.
В табл. 2 даны результаты идентификации модели (1).
Из табл. 2 видно, что адекватность модели (1) боковой линии нейлоидной формы комля очень высокая и по коэффициенту корреляции равна не меньше 0,8826. Максимальная теснота факторной связи рана 0,9995.
Таблица 2
Параметры модели формы комля березы на склоне лесного оврага
|
№ п/п |
Угол j, град |
D1.3, см |
P1.3, см |
Высота, м |
Параметры (1) формы комля |
Коэффициент корреляции |
|||||
|
h3 |
hmax |
H |
Hкр |
а |
b |
c |
|||||
|
1 |
20 |
20 |
85 |
0,81 |
0,70 |
25 |
20 |
6,69037 |
0,026546 |
83,04457 |
0,9932 |
|
2 |
18 |
20 |
90 |
0,64 |
0,66 |
24 |
15 |
1,51942 |
0,060980 |
87,94076 |
0,9609 |
|
3 |
15 |
15 |
70 |
0,60 |
0,69 |
19 |
13 |
1,57073 |
0,070650 |
71,08551 |
0,9995 |
|
4 |
15 |
18 |
70 |
0,35 |
0,50 |
24 |
17 |
14,29537 |
0,046288 |
68,62046 |
0,9876 |
|
5 |
15 |
20 |
74 |
0,36 |
0,40 |
25 |
19 |
5,36991 |
0,059820 |
73,78199 |
0,9984 |
|
7 |
20 |
20 |
87 |
0,35 |
0,70 |
20 |
10 |
5,53268 |
0,034759 |
86,94283 |
0,8826 |
|
8 |
30 |
25 |
75 |
0,40 |
0,80 |
16 |
12 |
8,65897 |
0,032264 |
75,13772 |
0,9985 |
|
9 |
20 |
20 |
61 |
0,48 |
0,90 |
20 |
14 |
7,58516 |
0,034666 |
61,50150 |
0,9790 |
|
10 |
15 |
35 |
88 |
0,36 |
1,15 |
25 |
9 |
26,87762 |
0,018077 |
85,23958 |
0,9973 |
|
11 |
15 |
20 |
56 |
0,40 |
1,20 |
18 |
8 |
15,87560 |
0,026839 |
55,55888 |
0,9992 |
|
12 |
20 |
24 |
65 |
0,40 |
1,15 |
15 |
10 |
5,53349 |
0,034409 |
64,18781 |
0,9792 |
|
13 |
20 |
20 |
53 |
0,41 |
1,20 |
20 |
15 |
34,54058 |
0,013320 |
46,87999 |
0,9992 |
|
14 |
20 |
20 |
62 |
0,35 |
1,17 |
19 |
10 |
15,16259 |
0,020174 |
60,74845 |
0,9974 |
|
15 |
15 |
27 |
91 |
0,45 |
1,30 |
18 |
7 |
25,34656 |
0,023777 |
89,19265 |
0,9904 |
|
16 |
20 |
28 |
85 |
0,38 |
1,15 |
15 |
9 |
16,49362 |
0,025320 |
84,09267 |
0,9868 |
|
17 |
20 |
25 |
69 |
0,45 |
1,20 |
15 |
8 |
15,78504 |
0,022036 |
68,02200 |
0,9989 |
|
18 |
20 |
25 |
76 |
0,40 |
1,05 |
14 |
6 |
26,46798 |
0,011879 |
70,43326 |
0,9985 |
|
19 |
20 |
42 |
122 |
0,45 |
1,05 |
16 |
6 |
12,17655 |
0,040653 |
123,6581 |
0,9896 |
|
20 |
15 |
42 |
114 |
0,40 |
1,07 |
15 |
8 |
19,26593 |
0,026577 |
113,9366 |
0,9951 |
|
21 |
15 |
25 |
88 |
0,43 |
1,05 |
15 |
8 |
11,23616 |
0,024368 |
87,74433 |
0,9987 |
|
22 |
20 |
25 |
90 |
0,50 |
1,04 |
16 |
6 |
6,09201 |
0,025528 |
89,73489 |
0,9972 |
|
23 |
15 |
22 |
77 |
0,51 |
1,00 |
16 |
7 |
9,34285 |
0,020768 |
76,09297 |
0,9907 |
|
24 |
15 |
20 |
75 |
0,60 |
1,00 |
15 |
6 |
3,46519 |
0,032258 |
74,12755 |
0,9947 |
|
25 |
15 |
25 |
88 |
0,65 |
1,02 |
16 |
8 |
7,55135 |
0,022099 |
86,50699 |
0,9888 |
|
26 |
15 |
22 |
75 |
0,71 |
1,03 |
17 |
8 |
8,46063 |
0,018145 |
73,55011 |
0,9758 |
|
27 |
15 |
25 |
80 |
0,65 |
1,02 |
20 |
8 |
9,66769 |
0,025103 |
79,68765 |
0,9978 |
|
28 |
20 |
20 |
90 |
0,55 |
1,03 |
20 |
10 |
13,74723 |
0,014425 |
88,89935 |
0,9669 |
|
29 |
15 |
25 |
75 |
0,70 |
1,05 |
20 |
9 |
10,96744 |
0,018477 |
73,79080 |
0,9920 |
|
30 |
15 |
25 |
76 |
0,62 |
1,03 |
20 |
9 |
4,20086 |
0,033223 |
76,03804 |
0,9967 |
Общее уравнение тренда (тенденции), то есть детерминированной закономерности без учета волновых возмущений, для всех 7×3 = 21 факторных отношений имеет вид
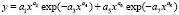 , (2)
, (2)
где y – показатель или зависимый фактор, в нашем примере параметры формулы (1); x – объясняющая переменная или влияющий фактор; a1… a8 – параметры модели (2), получаемые в программной среде CurveExpert.
Эта двухчленная формула в каждом случае выявления закономерности была получена идентификацией устойчивых законов по табл. 2. При этом первая составляющая, как правило, показывает естественный процесс или явление, а вторая и последующие члены формулы (2) характеризуют, как правило, антропогенное влияние.
В табл. 3 приведены результаты факторного влияния (по исходным данным из табл. 2) на значения параметров модели (1).
Таблица 3
Факторный анализ влияния параметров берез на параметры модели (1) по детерминированным биотехническим закономерностям
|
Параметра дерева (влияющий фактор x) |
Параметры формы комля |
Сумма коэфф. корр. |
Место Ix |
||
|
a |
b |
c |
|||
|
Угол местного склона j, град |
0,124 |
0,106 |
0,061 |
0,2910 |
7 |
|
Диаметр ствола D1.3, см |
0,367 |
0,652 |
0,7421 |
1,7611 |
1 |
|
Периметр ствола P1.3, см |
0,558 |
0,039 |
0,9951 |
1,5921 |
2 |
|
Высота при j = 0 комля h3, м |
0,474 |
0,009 |
0,081 |
0,5640 |
6 |
|
Высота при j > 0 комля hmax, м |
0,662 |
0,7395 |
0,025 |
1,4265 |
3 |
|
Высота дерева березы H, м |
0,068 |
0,364 |
0,133 |
0,5650 |
5 |
|
Высота кроны березы Hкр, м |
0,162 |
0,487 |
0,349 |
0,9980 |
4 |
|
Сумма коэффициента корреляции |
2,4150 |
2,3965 |
2,3862 |
7,1977 |
– |
|
Место Iy параметров модели |
1 |
2 |
3 |
– |
0,3427 |
На первом месте как влияющая переменная оказался диаметр на стандартной высоте, что указывает на правильность существующей в лесной таксации системы измерений лесных деревьев. Как зависимый показатель на первом месте находится первый параметр a формулы (1), то есть абсолютный сбег комля дерева.
Коэффициент коррелятивной вариации для всего множества влияния 7 влияющих переменных на три показателя равен 7,1977 / 21 = 0,3427.
Этот критерий (термин «коррелятивная вариация» по Ч. Дарвину) применяется при сравнении различных биологических объектов исследования, в данном случае группы из 29 берез, причем так можно сравнивать не только деревья и их группы в разных экологических условиях, но и растительные сообщества, находящие в разных местах произрастания.
Поэтому факторный анализ, проведенный по показателям одного и того же объекта исследования, имеет многогранное применение. Главное условие – это добротность и достоверность исходных данных. Тогда можно ожидать хороших результатов по выявлению биотехнических закономерностей между отдельными количественными факторами.
Из данных табл. 3 видно, что наибольшую тесноту связи с коэффициентом корреляции 0,9951 имеет влияние периметра ствола P1.3 (рис. 3) на изменение третьего параметра модели (1), то есть на свободного члена, имеющего размерность и смысл теоретического периметра поперечного сечения ствола дерева.
Почти предельно отсутствует факторная связь с наименьшим коэффициентом корреляции 0,009 влияния высоты комля вдоль продольной оси ствола на параметр b формулы (1), то есть на активность спада значений периметра или же на активность сбега боковой линии комля у учетных деревьев березы.
Ранее [1-5] нами была доказана волновая теория развития и роста деревьев.
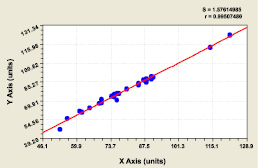
Рис. 3. Влияние периметра ствола P1.3 на изменение третьего параметра модели (1)
Поэтому проведена идентификация общей биотехнической закономерности
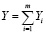 ,
,
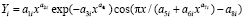 , (3)
, (3)
где Y – показатель, в нашем примере любой из трех параметров модели (1), i – номер члена общей формулы, m – количество составляющих общей формулы, шт., x – любой из семи влияющих переменных дерева и комля березы, a1… a8 – параметры одного члена формулы (4), физически представляемого как асимметричный вейвлет-сигнал с переменными амплитудой и частотой колебательного возмущения совокупности (популяции) из 29 берез.
Результаты идентификации модели (4) по статистическим данным из табл. 2 представлены в табл. 4.
При этом волновыми оказались четыре закономерности или 400 / 21 = 19,05 % от общего количества биотехнических закономерностей.
Коэффициенты корреляции волновых колебательных возмущений в виде вейвлет-сигналов в таблице 4 выделены крупным полужирным шрифтом.
С учетом принципа колебательной адаптации деревьев к условиям места своего произрастания на первое место среди параметров деревьев встала максимальная высота комля березы. Остальные шесть параметров остались в той же последовательности, что было при детерминированном представлении развития и роста древесных растений.
Таблица 4
Факторный анализ влияния параметров берез на параметры модели (1) по детерминированным и волновым биотехническим закономерностям
|
Параметра дерева (влияющий фактор x) |
Параметры формы комля |
Сумма коэфф. корреляции |
Место |
||
|
a |
b |
c |
|||
|
Угол местного склона j, град |
0,124 |
0,106 |
0,061 |
0,291 |
7 |
|
Диаметр ствола D1.3, см |
0,367 |
0,652 |
0,7421 |
1,7611 |
2 |
|
Периметр ствола P1.3, см |
0,558 |
0,039 |
0,9951 |
1,5921 |
3 |
|
Высота при j=0 комля h3, м |
0,474 |
0,009 |
0,081 |
0,56+4 |
6 |
|
Высота при j>0 комля hmax, м |
0,7716 |
0,8820 |
0,7444 |
2,3980 |
1 |
|
Высота дерева березы H, м |
0,068 |
0,364 |
0,133 |
0,5650 |
5 |
|
Высота кроны березы Hкр, м |
0,162 |
0,7093 |
0,349 |
1,2203 |
4 |
|
Сумма коэффициента корреляции |
2,5246 |
2,7613 |
3,1056 |
8,3915 |
– |
|
Место Iy параметров модели |
3 |
2 |
1 |
– |
0,3996 |
Коэффициент коррелятивной вариации, из-за волнового влияния максимальной высоты комля и высоты кроны дерева на формирование комля, повысился на 100(0,3996 – 0,3427) / 0,3427 = 16,55 %.
Иерархия показателей a, b и c по сравнению с табл. 3 перевернулась и стала в новом рейтинге колебательного возмущения последовательностью c, b и a. В этом случае теоретический периметр поперечного сечения ствола на высоте 1,3 м оказывается наиболее значимым зависимым показателем. Это позволит в будущем обратить особое внимание на соотношение периметра к диаметру для выявления закономерностей изменения формы поперечного сечения ствола на стандартной высоте 1,3 м.
Таким образом, экологическая таксация деревьев коренным образом отличается от технической таксации стволов на древесину в виде кругляка. При этом модель (3) может быть доведена при моделировании по остаткам от предыдущих волновых составляющих даже ниже погрешности измерений.
Далее из табл. 4 выделим закономерности с убывающими значениями коэффициента корреляции, то есть, выполним ранжирование полученных биотехнических закономерностей по ухудшению их адекватности. В табл. 5 были оставлены только сильные связи, то есть закономерности с коэффициентами корреляции свыше 0,7. В итоге доля сильных факторных связей оказалось равной 100×6 / 21 = 28,57 %.
Таблица 5
Сильные факторные связи влияния параметров берез на параметры модели (1)
|
Параметра дерева (влияющий фактор x) |
Параметры формы комля |
||
|
a |
b |
c |
|
|
Диаметр ствола D1.3, см |
0,7421 |
||
|
Периметр ствола P1.3, см |
0,9951 |
||
|
Высота при j>0 комля hmax, м |
0,7716 |
0,8820 |
0,7444 |
|
Высота кроны березы Hкр, м |
0,7093 |
||
Из семи параметров деревьев березы три выпадают при уровне адекватности с коэффициентом корреляции выше 0,7. В итоге остаются только шесть закономерностей, которые приведем полностью в табл. 6 по убыванию их адекватности.
Таблица 6
Параметры общего уравнения (4) для сильных факторных связей
|
Номер i |
Вейвлет-сигнал |
|||||||
|
амплитуда колебания |
полупериод колебания |
сдвиг |
||||||
|
|
|
|
|
|
|
|
|
|
|
Влияние периметра ствола P1.3 на параметр c (рис. 3), коэффициент корреляции 0,9951 |
||||||||
|
1 |
0,81164 |
1,04444 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Влияние высоты комля hmax на параметр b (рис. 4), коэффициент корреляции 0,8820 |
||||||||
|
1 |
0,12751 |
0 |
1,51799 |
1,19775 |
0 |
0 |
0 |
0 |
|
2 |
-2,83740 |
15,61329 |
27,78498 |
1 |
0,038069 |
0,00014894 |
27,30161 |
2,39313 |
|
Влияние высоты комля hmax на параметр a (рис. 5), коэффициент корреляции 0,7716 |
||||||||
|
1 |
0,010269 |
0 |
-7,05156 |
0,50604 |
0 |
0 |
0 |
0 |
|
2 |
-0,21501 |
0 |
-2,99769 |
1 |
-3,17374 |
3,24198 |
0,0024367 |
2,50904 |
|
3 |
240,27165 |
0 |
5,036881 |
1 |
0,11780 |
0,025113 |
1,95649 |
5,43455 |
|
Влияние высоты комля hmax на параметр c (рис. 6), коэффициент корреляции 0,7444 |
||||||||
|
1 |
73,37379 |
0 |
-0,049923 |
0,40903 |
0 |
0 |
0 |
0 |
|
2 |
-4742,0259 |
2,57229 |
5,49302 |
0,0074645 |
0,66005 |
-0,29744 |
1,49662 |
-5,14666 |
|
Влияние диаметра ствола D1.3 на параметр c (рис. 7), коэффициент корреляции 0,7421 |
||||||||
|
1 |
46,33420 |
0 |
-0,021440 |
1 |
0 |
0 |
0 |
0 |
|
Влияние высоты кроны Hкр на параметр b (рис. 8), коэффициент корреляции 0,7093 |
||||||||
|
1 |
0,013306 |
0 |
-0,17573 |
0,70463 |
0 |
0 |
0 |
0 |
|
2 |
0,0021097 |
0 |
-0,17164 |
0,91488 |
7,44397 |
-0,15644 |
1,06891 |
-4,50361 |
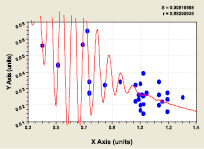
Рис. 4. Влияние высоты комля на параметр b
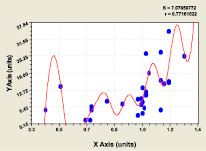
Рис. 5. Влияние высоты комля hmax на параметр a
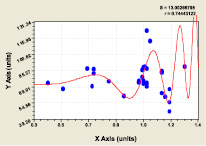
Рис. 6. Влияние высоты комля hmax на параметр c
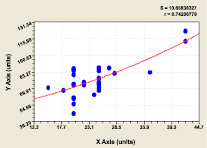
Рис. 7. Влияние диаметра ствола D1.3 на параметр c
Высокий уровень адекватности формы комля у всех 29 берез позволяет повести дальше полный факторный анализ параметров модели (1).
Для идентификации была применена общая формула (3).
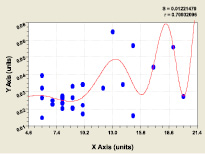
Рис. 8. Влияние высоты кроны Hкр на параметр b
Таким образом, предлагаемое техническое решение основано на результатах фундаментальных исследований влияния высоты поперечных сечений ствола и комля дерева на периметр этих сечений, а также влияния параметров комлевой части и высоты кроны лесных деревьев, произрастающих как единая популяция и как микро геотехническая система, десятилетиями на склоне оврага.
Оказалось, что угол местного склона почти не влияет на изучаемые показатели.
При этом измерения по предлагаемому способу просты в исполнении и наглядны для школьников при изучении деревьев в экологических кружках.
Поэтому предлагаемый способ измерения и анализа комля растущих на ровной местности или же на склонах оврагов, холмов, террас и берегов водных объектов может быть применен в индикации не только рельефа, но и фитоиндикации отдельных мест произрастания древесных растений на пробных площадях. Минимальное количество учетных деревьев определяется возможностью идентификации биотехнических закономерностей с волновыми составляющими и должно быть не менее 30 особей одного вида.
Библиографическая ссылка
Мазуркин П.М., Алгасова М.А. Закономерности формы комля дерева березы // Современные наукоемкие технологии. 2013. № 7-1. С. 101-107;URL: https://top-technologies.ru/ru/article/view?id=31919 (дата обращения: 13.03.2026).