Разработка интеллектуальных алгоритмов работы сложных систем является актуальной задачей современной инженерии, позволяющей создавать эффективные научные, промышленные и бытовые системы. Примерами таких систем являются автоматизированные системы управления промышленными и научными установками, цифровая телефония и офисная техника. В настоящее время известно множество интеллектуальных процедур управления, одной из которых является алгоритм самообучения нейронных сетей (НС) Хебба [1]. Представление управляющей системы в виде нейронной сети удобно в тех случаях, когда входная информация представляет собой параллельный поток или взаимосвязанную последовательность множества данных.
Целью исследования являлось определение параметров самообучения, обеспечивающих минимальное время обучения при сохранении заданного качества распознавания входных сигналов. Процедуры обучения нейронных сетей представляют собой правила, по которым изменяются весовые коэффициенты связей между нейронами. В процессе обучения нейронная сеть приобретает свойство формировать выходные сигналы соответствующие входным сигналам и позволяющие различать разные входные сигналы. Процесс обучения представляет собой циклическое повторение процедуры обучения до достижения заданного уровня правильности ответов. Количество повторов процедуры обучения в большинстве алгоритмов обучения определяется коэффициентом η, на который умножается величины поправок весовых коэффициентов, вычисленных в соответствии с алгоритмом обучения. Этот коэффициент называют скоростью обучения [1], и он отражает неопределенность алгоритма обучения. Во многих случаях этот коэффициент определяется экспериментально, так как он зависит и от параметров нейронной сети и от параметров распознаваемых сигналов. Слишком малые значения коэффициента η приводят к большому числу повторений цикла обучения, большие значения коэффициента приводят к потере устойчивости процесса обучения и невозможности достичь заданного качества обучения.
Алгоритм самообучения нейронных сетей (НС) Хебба основан на принципе усиления связи между возбужденными нейронами. Сигнальный метод обучения Хебба корректирует весовые коэффициенты НС в соответствии со следующими формулами [1]:
,
,
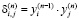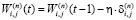где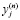 
– выходной сигнал обучаемого нейрона, 
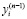– выходной сигнал нейрона предыдущего слоя, который является одним из входных сигналов обучаемого нейрона, h – коэффициент скорости самообучения, t – номер шага обучения, n – номер слоя НС, i, j – номера нейронов, 
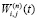– весовой коэффициент связи выхода i-го нейрона с входом j-го нейрона. В приведенных соотношениях не используется отрицательная обратная связь для ограничения роста весовых коэффициентов, что допустимо в случае проводимого исследования. Из формулы видно, что наибольшие изменения претерпит та синаптическая связь, которая соединяет большие входные и выходные сигналы. В матричной форме данный алгоритм можно записать в следующем виде [2]:
, 
,
,
, 
,
.
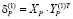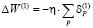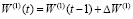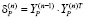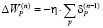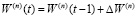Нейронная сеть Хебба самостоятельно определяет количество классов, на которые она разбивает поток обучающей выборки. В конце процесса обучения выходные сигналы нейронов выходного слоя должны иметь состояния близкие либо плюс единице, либо минус единице. Фактически, на выходе НС в конце обучения формируется двоичный код. Количество выходных линий НС должно браться с запасом, поскольку заранее количество классов неизвестно, при этом следует учитывать, что классы кодируются на выходе позиционным двоичным кодом.
Численное исследование процесса самообучения НС методом Хебба было основано на имитационной модели самообучающейся НС, которая должна решать задачу классификации заданного множества изображений нескольких символов. Каждому символу соответствует несколько несовпадающих между собой изображений, приведенные на рис. 1. Разрешение изображений: 10х6. Параметры НС имели следующие значения: количество слоев – 3, количество входов первого слоя – 60, количество нейронов по слоям – 16, 12, 5, начальная скорость обучения – 0,0005. Активационная функция нейронов представляла собой сигмоиду [1]. В качестве обучающей выборки были взяты 9 изображений трех цифр, приведенные на рис. 1. Начальные значения весовых коэффициентов задавались случайно, по равномерному закону распределения. Изображения каждой цифры отличаются за счет наложенных искажений. Классификация данных изображений для человека не вызывает трудностей.
Рис.1. Обучающая выборка
В качестве параметра для критерия завершенности процесса самообучения использовалась величина разности числа выходов НС и минимума модуля выходных сигналов.
,
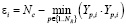где Nc – число выходов НС, равное числу бит выходного кода, p – номер изображения, Yp,i – выходной сигнал НС для p-го изображения на входе НС, i – номер шага самообучения. Критерий завершения процесса самообучения состоял в том, что при ei<eпороговое процесс самообучения завершался. В рассматриваемом примере число шагов самообучения не превышало 500. На рис. 2 показан процесс изменения модуля выходного сигнала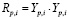 
для одного из входных сигналов (изображений) в процессе самообучения НС для различных коэффициентов скорости самообучения η.
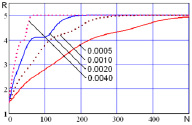
Рис. 2. Зависимость модуля выходного сигнала НС от номера шага обучения при различных значениях коэффициента скорости обучения h
В результате самообучения на выходе НС сформировалось множество выходных сигналов, представленное на рис. 3. Каждый столбик приведенной диаграммы представляет собой число, соответствующее 5-битовому числу от 0 до 31, получаемому на выходе НС, если считать, что каждый выход соответствует определенному разряду двоичного кода числа.
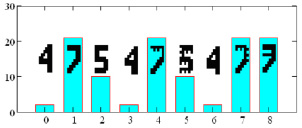
Рис. 3. Множество выходных кодов и соответствующие символы на входе НС
Сопоставление рис. 1 и 3 позволяет сделать заключение, что нейронная сеть правильно осуществляет классификацию изображений цифр для использованных изображений. Столбики 1, 4, 7 соответствуют различным вариантам изображения цифры «4», столбики 2, 5, 8, 9 – изображения цифры «7», столбики 3, 6 – изображения цифры «5».
Варьирование в процессе численного моделирования коэффициента скорости самообучения h в пределах 0,0005-0,0040 позволило установить, что при величинах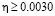 
число разных выходных кодов уменьшается с 3 до 2, то есть нейронная сеть перестает различать два разных символа. Для диапазона 
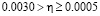изменений выходного кода отмечено не было.
Успешность самообучения зависит от начальных значений матриц весовых коэффициентов. В результате численных экспериментов было установлено, что число классов, определяемых нейронной сетью для неизменной группы распознаваемых изображений для разных случайных начальных значений весовых матриц W может быть и завышенным или заниженным относительно числа, установленного экспертом.
Распознавание группы символов в условиях, когда заранее не известно их количество, требуется в задачах автоматического чтения текстов и схем на этапе установления численности символов используемого алфавита.
Из приведенных результатов можно сделать следующие выводы:
Коэффициент скорости самообучения НС по алгоритму Хебба влияет на количество различных выходных кодов: увеличение скорости самообучения выше некоторого порога приводит к уменьшению количества распознаваемых классов.
Коэффициент скорости самообучения НС не влияет на численные значения выходных двоичных кодов.
Библиографическая ссылка
Капля В.И., Чернуха В.В. ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПРОЦЕССА САМООБУЧЕНИЯ НЕЙРОННЫХ СЕТЕЙ МЕТОДОМ ХЕББА ОТ ВЕЛИЧИНЫ КОЭФФИЦИЕНТА СКОРОСТИ ОБУЧЕНИЯ // Современные наукоемкие технологии. – 2013. – № 5. – С. 62-64;URL: https://top-technologies.ru/ru/article/view?id=31801 (дата обращения: 26.12.2024).