В общем случае гибридные фрактальные структуры, вложенные в единичный объем 3D пространства, могут быть образованы тремя разными генераторами. Для символьного описания возможных классов мономодулярных гибридных фрактальных структур с тремя генераторами будем использовать следующие обозначения:
F(Gx, Gy, Gz){dsp, (dFrag, yz , dFrag, xz , dFrag, xy), (dgen, x, dgen, y, dgen, z)},
где F(Gx, Gy, Gz) – обозначение гибридного фрактала с указанием всех его генераторов, dsp , dFrag, yz , dFrag, xz и dFrag, xy – топологические размерности пространства существования фрактала и структурных фрагментов в соответствующих взаимно ортогональных 2D-подпространствах, dgen, x, dgen, y и dgen,z – топологические размерности соответствующих генераторов. Области возможных значений: dFrag, yz (xz, xy) [0,1,2], dgen, x (y, z) [0,1,2].
Тогда в 3D-пространстве возможны следующие варианты точечных гибридных фрактальных структур с тремя разными генераторами Gx, Gy и Gz:
1) F(Gx, Gy, Gz){3, (0,0,0), (0,0,0)},
2) F(Gx, Gy, Gz){3, (0,0,0), (0,0,1)},
3) F(Gx, Gy, Gz){3, (0,0,0), (0,1,1)},
4) F(Gx, Gy, Gz){3, (0,0,0), (1,1,1)},
Формально возможные варианты линейчатых гибридных фрактальных структур с двумя генераторами, например, Gx, и Gy, следующие:
1) F(Gx, Gy, Z){3, (0,1,1), (0,0, -)},
2) F(Gx, Gy, Z){3, (0,1,1), (0,1, -)},
3) F(Gx, Gy, Z){3, (0,1,1), (1,1, -)}.
Фрактальные структуры из упорядоченных по фрактальному закону фрагментов плоскости F(Gx,Y,Z){3,(1,2,2),(0,-,-)} и F(Gx,Y,Z){3,(1,2,2),(1,-,-)} не являются гибридными.
Гибридные линейчатые структуры с тремя генераторами Gx, Gy и G*z, где G*z – генератор фрактальной линии, совместимый по свойствам с генератором Gx (Gy), могут быть следующие:
1) F(Gx, Gy, G*z){3,(0,1,1),(0,0,1)},
2) F(Gx, Gy, G*z){3,(0,1,1),(0,1,1)},
3) F(Gx, Gy, G*z){3,(0,1,1),(1,1,1)}.
Отметим, что под совместимостью линейного генератора G*z с одним из точечных Gx (или Gy) понимается изоморфизм его сечения плоскостью ZX (или ZY) с ним, т.е. G*z|ZX(ZY) → G*x(y) ↔ Gx(y).
Гибридные структуры из фрактальных поверхностей, упорядоченных а единичном объеме 3D пространства по фрактальному закону Gx и совместимых с ним:
1) F(Gx, G*yz){3,(1,2,2),(0,2)},
2) F(Gx, G*yz){3,(1,2,2),(1,2)}.
Условие совместимости:
G*zy|ZX(ZY) → G*z ↔ Gx.
В 2D-пространстве имеем следующие возможные варианты точечных гибридных фрактальных структур с двумя генераторами, например, Gx, и Gy:
1) F(Gx,Gy){2,(0,1),(0,0)},
2) F(Gx,Gy){2,(0,1),(0,1)},
3) F(Gx,Gy){2,(0,0),(1,1)}.
Возможные линейчатые гибридные фрактальные структуры в 2D-пространстве с двумя генераторами Gx, и G*z, где G*z – генератор фрактальной линии, совместимый по свойствам с генератором Gx:
1) F(Gx, G*z){2,(0,1),(0,1)}
В качестве примера возможности существования последнего варианта гибридной структуры можно привести линейчатую фрактальную структуру с генератором G*z типа треугольной кривой Коха и совместимым с ним генератором Gx типа канторова множества точек (рисунок).
Между точечными структурами 2D-пространства и линейчатыми структурами 3D-пространства существуют очевидные связи:
SvZ F(Gx, Gy, Z){3, (0,1,1), (0,0,-)} = F(Gx, Gy){2, (0,0), (0,0)},
SvZ F(Gx, Gy, Z){3, (0,1,1), (0,1,-)} = F(Gx, Gy){2, (0,0), (0,1)},
SvZ F(Gx, Gy, Z){3, (0,1,1), (1,1,-)} = F(Gx, Gy){2, (0,0), (1,1)}.
Между точечными структурами 1D-пространства, линейчатыми структурами и структурами 3D-пространства из фрагментов поверхности также существуют очевидные связи:
SvYZ F(Gx, Y, Z){3, (1,2,2), (0,-,-)} = F(Gx){1, (0), (0)},
SvYZ F(Gx, Y, Z){3, (1,2,2), (1,-,-)} = F(Gx){1, (0), (1)}.
Определим фрактальные размерности выведенных структур через размерности их генераторов. Тогда фрактальные размерности точечных, линейчатых структур и структур из фрагментов поверхности могут быть соответственно представлены следующим образом:
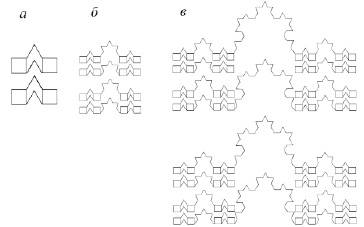
Изображения генератора гибридного линейчатого фрактала F(Gx, G*z){2,(0,1),(0,1)} (а) и предфрактальных гибридных структур 2-го (б) и 3-го поколения в 2D пространстве
Dim F(Gx, Gy, Gz) = Dim F1(Gx) + Dim F2(Gx) + Dim F3(Gx),
Dim F(Gx, Gy, Z) = 1 + Dim F(Gx, Gy) = 1 + Dim F1(Gx) + Dim F2(Gx).
Dim F(Gx, Y, Z) = 2 + Dim F(Gx).
Dim F(Gx, Gy, G*z) = Dim F1(Gx) + Dim F2(Gx) + Dim F3(G*x),
Dim F(Gx, G*yz) = Dim F(Gx) + Dim F(G*yz).
Таким образом, проанализирована возможность существования и определены размерности вероятных гибридных мономодулярных (точечных, линейчатых и из фрагментов поверхности) фрактальных структур в 3D-пространстве.
Библиографическая ссылка
Иванов В.В. ОБЩАЯ ХАРАКТЕРИСТИКА ВОЗМОЖНЫХ ГИБРИДНЫХ МОНОМОДУЛЯРНЫХ ФРАКТАЛЬНЫХ СТРУКТУР // Современные наукоемкие технологии. 2013. № 5. С. 29-31;URL: https://top-technologies.ru/ru/article/view?id=31795 (дата обращения: 07.03.2026).



